Qui aura 20 en maths ?
💯 Teste ton niveau de maths et tente de gagner un des lots !S'inscrire au jeu →
Nouveau
🔥 Découvre nos fiches d'exercices gratuites avec corrections en vidéo !Accéder aux fiches →
Sujet 1 - Exercice 1
20 min
40
Olivia s’est acheté un tableau pour décorer le mur de son salon. Ce tableau, représenté ci-contre, est constitué de quatre rectangles identiques nommés et dessinés à l’intérieur d’un grand rectangle d’aire égale à
Le ratio longueur : largeur est égale à pour chacun des cinq rectangles.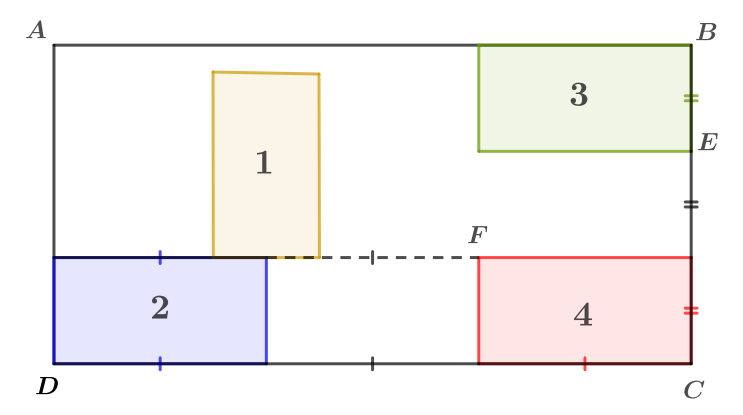
Le ratio longueur : largeur est égale à pour chacun des cinq rectangles.

Question 1
Recopier, en les complétant, les phrases suivantes. Aucune justification n’est demandée.
Le rectangle est l’image du rectangle par la translation qui transforme en
Correction
- Définition : Transformer une figure par translation, c’est la faire glisser sans la tourner ni la déformer. Le glissement se fait selon :
- Une direction
- Un sens
- Une longueur.
Question 2
Le rectangle est l’image du rectangle par la rotation de centre et d’angle dans le sens des aiguilles d’une montre.
Correction
- Définition : Transformer une figure par rotation revient à la faire tourner (pivoter) autour d’un point. La figure tourne (pivote) selon :
- Une mesure d'angle donnée.
- Un sens direct ou indirect : (sens anti-horaire ou sens horaire.)
Question 3
Le rectangle est l’image du rectangle par l’homothétie de centre et de rapport
(Il y a plusieurs réponses possibles, une seule est demandée).
(Il y a plusieurs réponses possibles, une seule est demandée).
Correction
Le rectangle est l’image du rectangle par l’homothétie de centre et de rapport
Le rectangle est l’image du rectangle par l’homothétie de centre et de rapport
Le rectangle est l’image du rectangle par l’homothétie de centre et de rapport
Question 4
Quelle est l’aire d’un petit rectangle ?
Correction
À la question précédente, on a justifié que Le rectangle est l’image du rectangle par l’homothétie de centre et de rapport
Autrement dit, le rectangle est une réduction du triangle de rapport
Par conséquent
D'après l'énoncé, l'aire du rectangle est égale à D'où :
On peut donc conclure que l'aire d'un petit rectangle est de
Autrement dit, le rectangle est une réduction du triangle de rapport
- Lorsque les dimensions d’une figure sont multipliées par un nombre positif , nous obtenons une nouvelle figure dont l’aire est multipliée par
D'après l'énoncé, l'aire du rectangle est égale à D'où :
On peut donc conclure que l'aire d'un petit rectangle est de
Question 5
Quelles sont la longueur et la largeur du rectangle
Correction
- Deux nombres sont dans le ratio 3 : 2 si on a l'égalité suivante :
On a alors En utilisant la règle du produit en croix, on a :
Ici, on va déterminer en fonction de :
Ici, on divise chaque membre de l'égalité par
On sait que l'aire du rectangle est de
Or , on a donc :
Ici on divise chaque membre de l'égalité par
Or par conséquent :