Nouveau

🔥 Découvre nos fiches d'exercices gratuites avec corrections en vidéo !Accéder aux fiches  →

Fonction linéaire

Sujet 1 - Exercice 1

1 min
0
L’eau en gelant augmente de volume. Le segment de droite ci-dessous représente le volume de glace (en litres) obtenu à partir d’un volume d’eau liquide (en litres).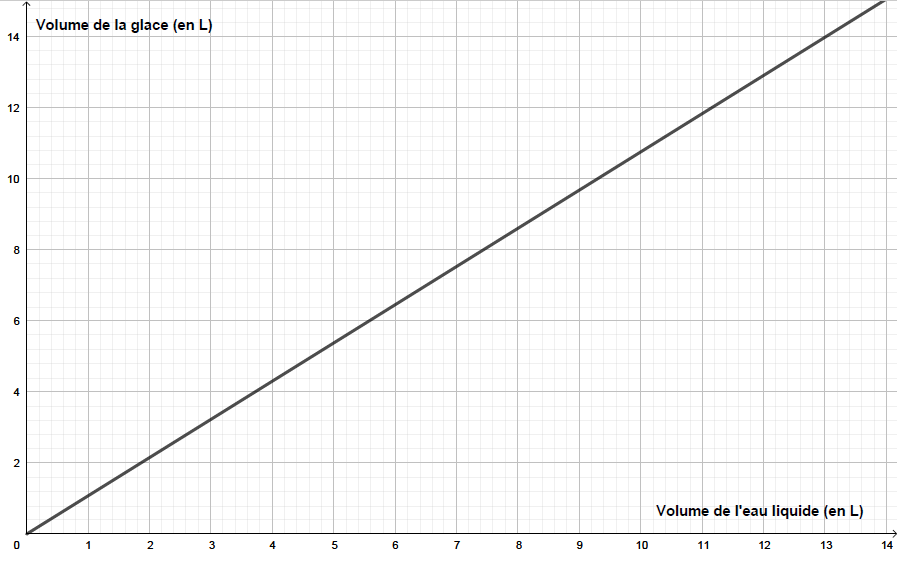
Question 1
En utilisant le graphique, répondre aux questions suivantes.

Quel est le volume de glace obtenu à partir de 66 litres de liquide d'eau ?

Correction
A l'aide du graphique ci-dessous, on peut en déduire qu'à partir de 66 litres de liquide d'eau, on peut obtenir environ 6.5\color{red}6.5 litres de glace.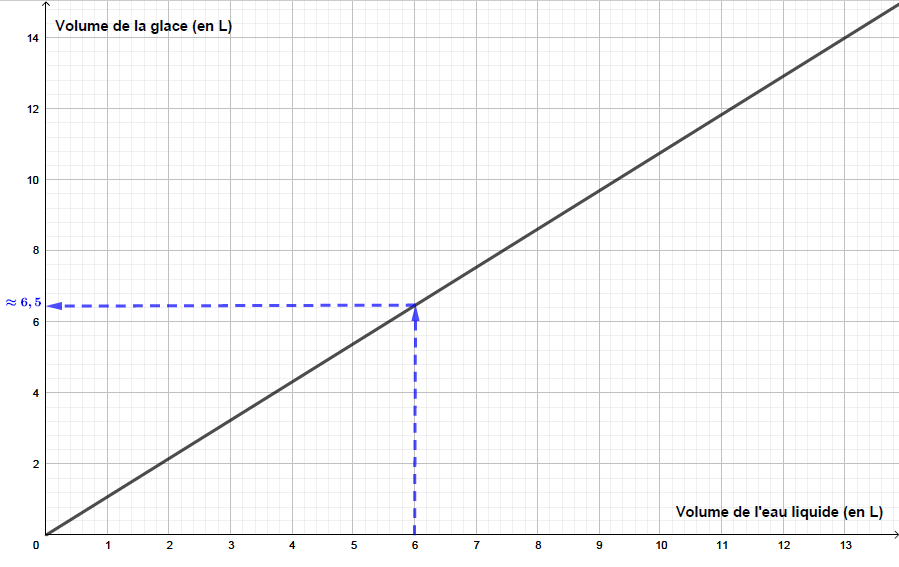
Question 2

Quel volume d’eau liquide faut-il mettre à geler pour obtenir 1010 litres de glace ?

Correction
A l'aide du graphique ci-dessous, on peut en déduire qu'il faut mettre 9,4 litres d'eau pour obtenir 1010 litres de glace.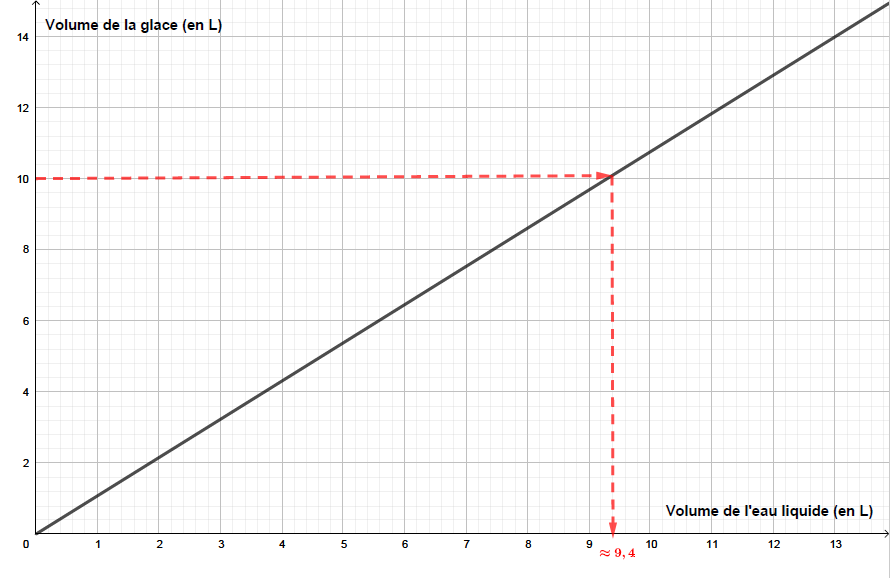
Question 3

Le volume de glace est-il proportionnel au volume d’eau liquide ? Justifier

Correction
  • La représentation graphique d'une fonction linéaire est une droite qui passe par l'origine du repère.
Ici, on a bien une droite qui passe par l'origine du repère, par conséquent, on peut conclure que le volume de glace est bien proportionnel au volume d’eau liquide.
Question 4

On admet que 1010 litres d’eau donnent 10,810,8 litres de glace. De quel pourcentage ce volume d’eau augmente-t-il en gelant ?

Correction
  • Calculer un pourcentage, c'est donner une proportion sous forme d'une fraction.
    La fraction doit être de dénominateur 100.
  • Pour calculer la proportion d’un nombre A par rapport à un nombre total B :
  • On utilise la formule suivante   \; ⟹\color{red}\Longrightarrow   \;pourcentage=nombre  Anombre  total  B×100\color{red}\boxed{pourcentage=\frac{nombre\; A}{nombre\; total \;B}\times {100}}
On admet que 1010 litres d’eau donnent 10,810,8 litres de glace.
Pour 1010 litres d'eau, on a une augmentation de 0,80,8 litre donc :
pourcentage=nombre  Anombre  total  B×100pourcentage=\frac{nombre\; A}{nombre\; total \;B}\times {100}
pourcentage=0,810×100pourcentage=\frac{0,8}{10}\times {100}
pourcentage≈8%\boxed{pourcentage\approx 8\%}
On peut donc conclure ici que le volume d'eau augmente de 8%\color{blue}8\% en gelant.