Qui aura 20 en maths ?

💯 Teste ton niveau de maths et tente de gagner un des lots !S'inscrire au jeu  →

Nouveau

🔥 Découvre nos fiches d'exercices gratuites avec corrections en vidéo !Accéder aux fiches  →

Exercices types : 22ème partie - Exercice 1

16 min
30
Question 1
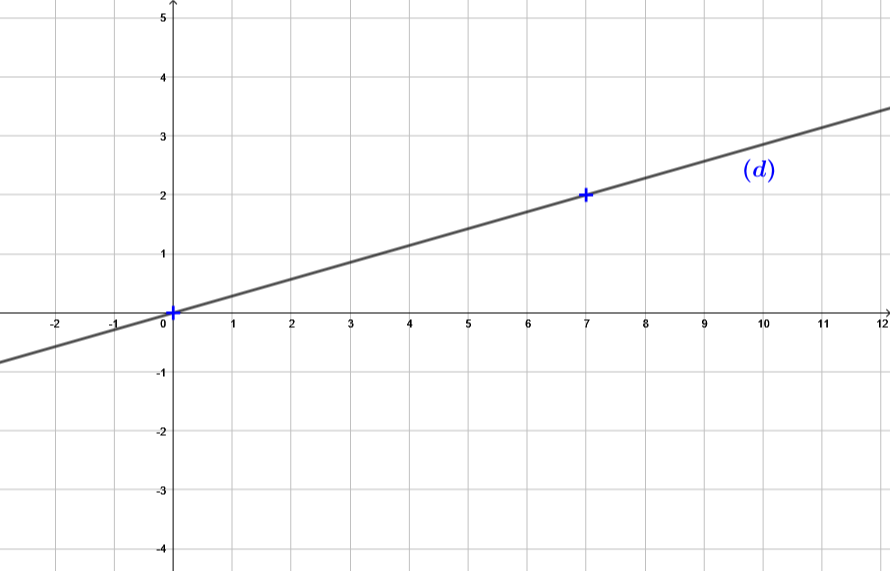
Une droite (d)(d) représente la fonction linéaire ff telle que f(x)=−3,5xf (x) = -3,5x

Dans un repère, représenter graphiquement la droite (d)(d).

Correction
  • La représentation graphique d'une fonction linéaire est une droite qui passe par l'origine du repère.
Pour tracer la droite (d) on a besoin de 2 points :
  • On connait déjà un premier point, de coordonnée (0;0)\color{blue}(0;0), car la droite (d)(d) est la représentation graphique d'une fonction linéaire.
  • Afin de déterminer les coordonnées d'un autre point de la droite (d)(d), il suffit de calculer l'image d'un point quelconque.
    Calculons ici l'image du point d’abscisse −‾\underline{-}2 :
    (Ici, on peut choisir n'importe quel autre abscisse.)
    Pour déterminer l'image de −2-2 par ff, il nous suffit de remplacer xx par −2-2.
    Il vient alors que :
    f(−2)=−3,5×(−2)f\left(-2\right)=-3,5\times (-2)
    f(−2)=7f\left(-2\right)=7

    L'image de −2-2 par ff vaut 77.
    Donc ici, on a bien les coordonnées d'un 2eˋme2^{ème} points : (−2;7)\color{blue}(-2;7).
    • Question 2

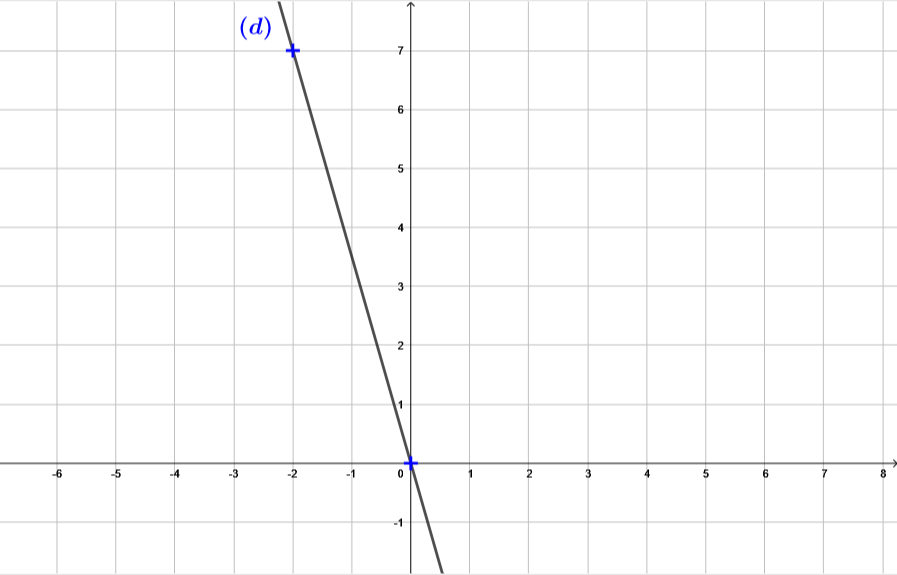
    Représenter graphiquement la fonction linéaire suivante : g(x)=3xg(x)=3x

    Correction
    • La représentation graphique d'une fonction linéaire est une droite qui passe par l'origine du repère.
    Pour tracer la droite (d) on a besoin de 2 points :
  • On connait déjà un premier point, de coordonnée (0;0)\color{blue}(0;0) car la droite (d)(d) est la représentation graphique d'une fonction linéaire.
  • Afin de déterminer les coordonnées d'un autre point de la droite (d)(d), il suffit de calculer l'image d'un point quelconque.
    Calculons ici l'image du point d’abscisse −‾\underline{-}1 :
    ( Ici on peut choisir n'importe quel autre abscisse.)
    Pour déterminer l'image de 11 par gg, il nous suffit de remplacer xx par 11.
    Il vient alors que :
    g(1)=3×1g\left(1\right)=3\times 1
    g(1)=3g\left(1\right)=3

    L'image de 11 par gg vaut 33 .
    Donc ici on a bien les coordonnées d'un 2eˋme2^{ème} points : (1;3)\color{blue}(1;3).
    • Question 3

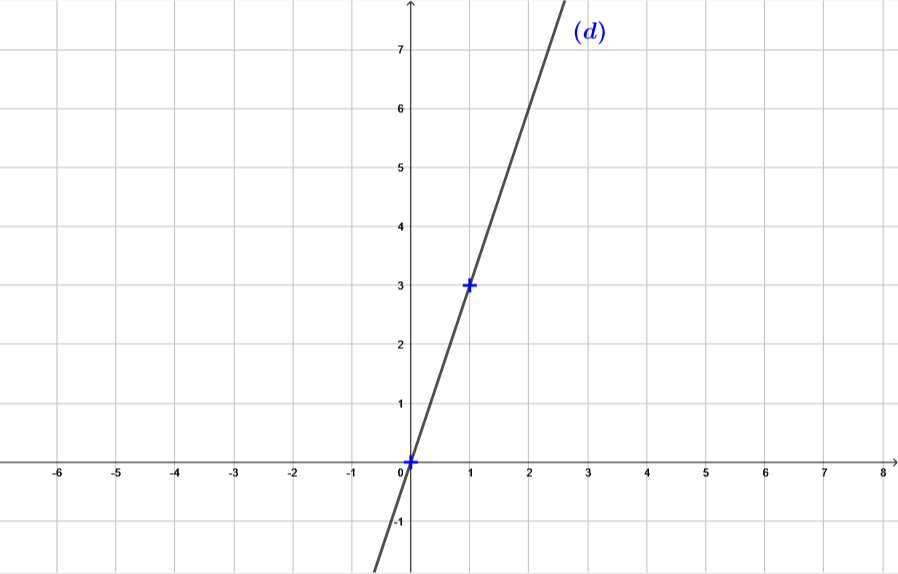
    Représenter graphiquement la fonction linéaire suivante : h(x)=27xh(x)=\frac{2}{7}x

    Correction
    • La représentation graphique d'une fonction linéaire est une droite qui passe par l'origine du repère.
    Pour tracer la droite (d) on a besoin de 2 points :
  • On connait déjà un premier point, de coordonnée (0;0)\color{blue}(0;0) car la droite (d)(d) est la représentation graphique d'une fonction linéaire.
  • Afin de déterminer les coordonnées d'un autre point de la droite (d)(d), il suffit de calculer l'image d'un point quelconque.
    Calculons ici l'image du point d’abscisse 77 :
    ( Ici on peut choisir n'importe quel autre abscisse.)
    Pour déterminer l'image de 77 par hh, il nous suffit de remplacer xx par 77.
    Il vient alors que :
    h(7)=27×7h\left(7\right)=\frac{2}{7}\times 7
    h(7)=2h\left(7\right)=2

    L'image de 77 par hh vaut 22 .
    Donc ici on a bien les coordonnées d'un 2eˋme2^{ème} points : (7;2)\color{blue}(7;2).