Nouveau
🔥 Découvre nos fiches d'exercices gratuites avec corrections en vidéo !Accéder aux fiches →
Tchat avec un prof
🤔 Bloqué sur un exercice ou une notion de cours ? Échange avec un prof sur le tchat !Découvrir →
Sujet 2 - Exercice 1
25 min
45
Question 1
Un sondage est mené auprès de clients d’un magasin de téléphonie mobile ayant acheté un téléphone (et un seul) de modèle ou de modèle avec deux choix de forfaits possibles :
forfait : « Internet mobile » ou forfait :« Internet mobile ».
Le téléphone de modèle coûte moins cher que le téléphone de modèle et le coût du forfait est moins élevé que celui du forfait .
Sur les clients sondés, ont souscrit un forfait et ont acheté un téléphone de modèle
On relève également que des sondés ayant acheté un téléphone de modèle ont souscrit un forfait
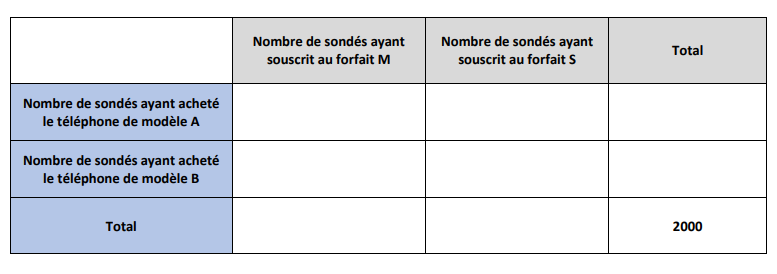
A l’aide des données précédentes, compléter le tableau croisé d’effectifs ci-dessous.
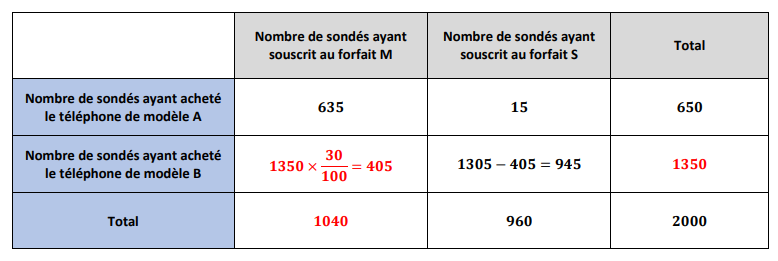
Correction
Question 2
Quelle est la fréquence des sondés ayant souscrit un forfait ?
Correction
Nous allons commencer par calculer la probabilité des sondés ayant souscrit un forfait . Nous traduirons ensuite le résultat en fréquence.
. Nous allons simplifier l'écriture de la fraction rationnelle . Il vient alors que :
Il en résulte donc que la fréquence des sondés ayant souscrit un forfait est de .
. Nous allons simplifier l'écriture de la fraction rationnelle . Il vient alors que :
Il en résulte donc que la fréquence des sondés ayant souscrit un forfait est de .
Question 3
Quelle est la fréquence des sondés qui ont acheté un téléphone de modèle et ont souscrit un forfait ?
Correction
Nous allons commencer par calculer la probabilité des sondés qui ont acheté un téléphone de modèle et ont souscrit un forfait . Nous traduirons ensuite le résultat en fréquence.
La probabilité des sondés qui ont acheté un téléphone de modèle et ont souscrit un forfait
L'évènement correspond à l'évènement : le sondé a acheté un téléphone de modèle ont souscrit un forfait
Dans le tableau, nous lisons qu'il y a personnes sur les qui ont acheté un téléphone de modèle et ont souscrit un forfait . On peut alors écrire que :
. Nous allons simplifier l'écriture de la fraction rationnelle . Il vient alors que :
La fréquence des sondés qui ont acheté un téléphone de modèle et ont souscrit un forfait est de .
La probabilité des sondés qui ont acheté un téléphone de modèle et ont souscrit un forfait
L'évènement correspond à l'évènement : le sondé a acheté un téléphone de modèle ont souscrit un forfait
Dans le tableau, nous lisons qu'il y a personnes sur les qui ont acheté un téléphone de modèle et ont souscrit un forfait . On peut alors écrire que :
. Nous allons simplifier l'écriture de la fraction rationnelle . Il vient alors que :
La fréquence des sondés qui ont acheté un téléphone de modèle et ont souscrit un forfait est de .
Question 4
L’affirmation suivante du directeur de cette agence est-elle vraie ?
« Moins d’un tiers des sondés choisit la formule la plus économique »
« Moins d’un tiers des sondés choisit la formule la plus économique »
Correction
Nous souhaitons ici déterminer la probabilité de l'évènement .
. Nous allons simplifier l'écriture de la fraction rationnelle . Il vient alors que :
Or à près.
Ainsi :
L’affirmation du directeur de cette agence n'est pas vraie.
. Nous allons simplifier l'écriture de la fraction rationnelle . Il vient alors que :
Or à près.
Ainsi :
L’affirmation du directeur de cette agence n'est pas vraie.
Question 5
Si on choisit au hasard un client parmi les sondés qui ont répondu avoir souscrit un forfait
est-il vrai qu’il y a une très forte probabilité qu’il ait acheté un téléphone de modèle ?
est-il vrai qu’il y a une très forte probabilité qu’il ait acheté un téléphone de modèle ?
Correction
Cette affirmation est une probabilité conditionnelle.
On pourrait traduire la question de la manière suivante ; que le sondé a souscrit un forfait quelle est la probabilité qu'il ait acheté un téléphone de modèle
Le résultat est une probabilité qui est très proche de .
Il est alors vrai que si un client parmi les sondés a répondu avoir souscrit un forfait alors il est vrai qu’il y a une très forte probabilité qu’il ait acheté un téléphone de modèle .
On pourrait traduire la question de la manière suivante ; que le sondé a souscrit un forfait quelle est la probabilité qu'il ait acheté un téléphone de modèle
Le résultat est une probabilité qui est très proche de .
Il est alors vrai que si un client parmi les sondés a répondu avoir souscrit un forfait alors il est vrai qu’il y a une très forte probabilité qu’il ait acheté un téléphone de modèle .
Question 6
Dans un autre magasin de téléphonie mobile, une enquête de satisfaction proposée à chaque client a donné les résultats suivants :
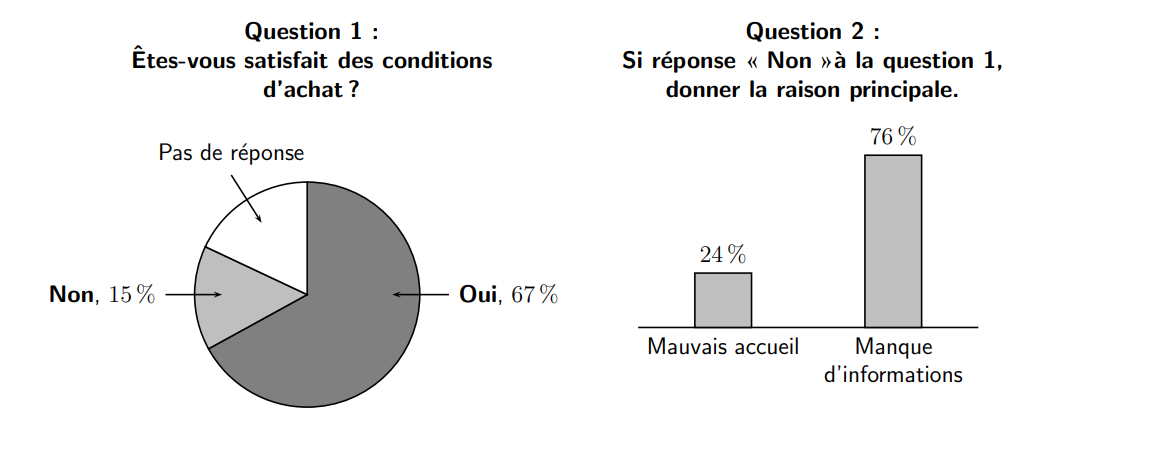
Quelle est la proportion, exprimée en pourcentage, de clients interrogés qui n’ont pas répondu à la première question ?
Correction
Le diagramme circulaire entièrement rempli correspond à .
Il en résulte donc que :
des clients interrogés n’ont pas répondu à la première question.
Il en résulte donc que :
des clients interrogés n’ont pas répondu à la première question.
Question 7
Parmi l’ensemble des clients interrogés, quelle est la proportion, exprimée en pourcentage, de ceux qui ne sont pas satisfaits des conditions d’achat en raison d’un mauvais accueil ?
Correction
- On considère une population , une sous-population de et une sous-population de .
On note la proportion d'individus de la population dans et la proportion d'individus de la population dans .
La sous-population ici correspond à ceux qui ont dit NON et ainsi
La sous-population ici correspond à la proportion de ceux qui ont eu un mauvais accueil parmi ceux qui ont dit NON, il vient alors que
La proportion d'individus de dans c'est à dire parmi l’ensemble des clients interrogés, exprimée en pourcentage, de ceux qui ne sont pas satisfaits des conditions d’achat en raison d’un mauvais accueil vaut :
Ainsi :
Parmi l’ensemble des clients interrogés, ne sont pas satisfaits des conditions d’achat en raison d’un mauvais accueil.
Signaler une erreur
Aide-nous à améliorer nos contenus en signalant les erreurs ou problèmes que tu penses avoir trouvés.
Connecte-toi ou crée un compte pour signaler une erreur.