Qui aura 20 en maths ?

💯 Teste ton niveau de maths et tente de gagner un des lots !S'inscrire au jeu  →

Nouveau

🔥 Découvre nos fiches d'exercices gratuites avec corrections en vidéo !Accéder aux fiches  →

Calculer des probabilités avec un tableau croisé d'effectifs : 1ère partie - Exercice 2

10 min
20
Dans un lycée, il y a 150150 élèves de Première technologique qui se répartissent comme indique le tableau ci-dessous :
Question 1
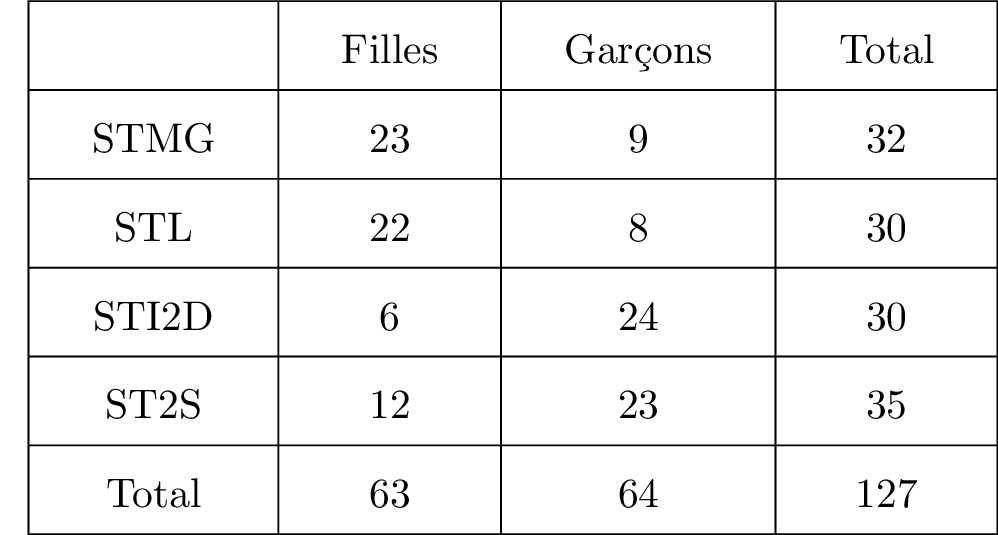
On considère les événements suivants :
  • AA : " l'élève est une fille ".
  • BB : " l'élève est un garçon ".
  • CC : " l'élève est en STMG".
  • DD : " l'élève est en STL".
  • EE : " l'élève est en STI2D".
  • FF : " l'élève est en ST2S".
On tire au hasard un élève .

Calculer la probabilité de l'évènement CC .

Correction
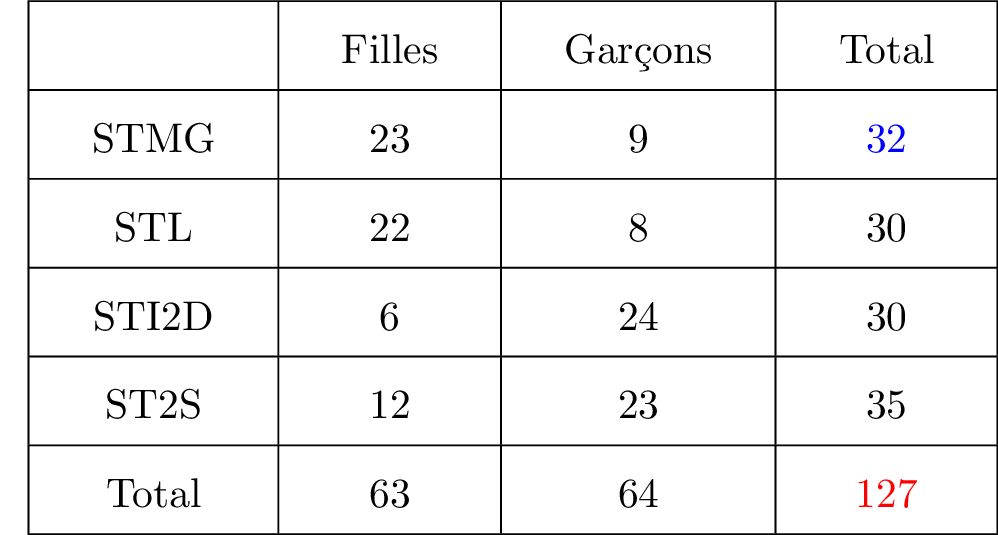
p(C)=nombre des issues favorables pour Cnombre des issues possiblesp\left(C\right)=\frac{\blue{\text{nombre des issues favorables pour }C}}{\red{\text{nombre des issues possibles}}}
p(C)=32127p\left(C\right)=\frac{\color{blue}32}{\color{red}127}
Question 2

Traduire par une phrase l'évènement B∩EB\cap E et calculer sa probabilité.

Correction
L'évènement B∩EB\cap E correspond à l'évènement : l’ordinateur est un garçon et{\color{blue}{\text{et}}} l'élève est en STI2D.
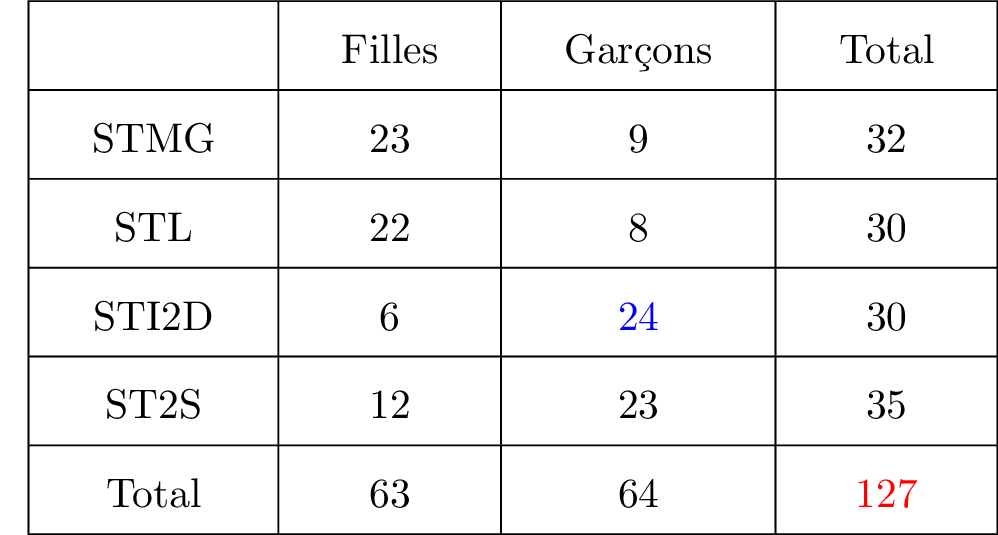
p(B∩E)=24127p\left(B\cap E\right)=\frac{\color{blue}24}{\color{red}127}
Question 3

Traduire par une phrase l'évènement B∪EB\cup E et calculer sa probabilité.

Correction
L'évènement B∪EB\cup E correspond à l'évènement : l’ordinateur est un garçon ou{\color{blue}{\text{ou}}} l'élève est en STI2D.
  • P(A∪B)=P(A)+P(B)−P(A∩B)P\left(A\cup B\right)=P\left(A\right)+P\left(B\right)-P\left(A\cap B\right)
P(B∪E)=P(B)+P(E)−P(B∩E)P\left(B\cup E\right)=P\left(B\right)+P\left(E\right)-P\left(B\cap E\right) équivaut successivement à :
P(B∪E)=64127+30127−24127P\left(B\cup E\right)=\frac{64}{127}+\frac{30}{127}-\frac{24}{127}
P(B∪E)=70127P\left(B\cup E\right)=\frac{70}{127}