Qui aura 20 en maths ?

💯 Teste ton niveau de maths et tente de gagner un des lots !S'inscrire au jeu  →

Nouveau

🔥 Découvre nos fiches d'exercices gratuites avec corrections en vidéo !Accéder aux fiches  →

Comment étudier la périodicité d'une fonction - Exercice 2

5 min
15
Question 1

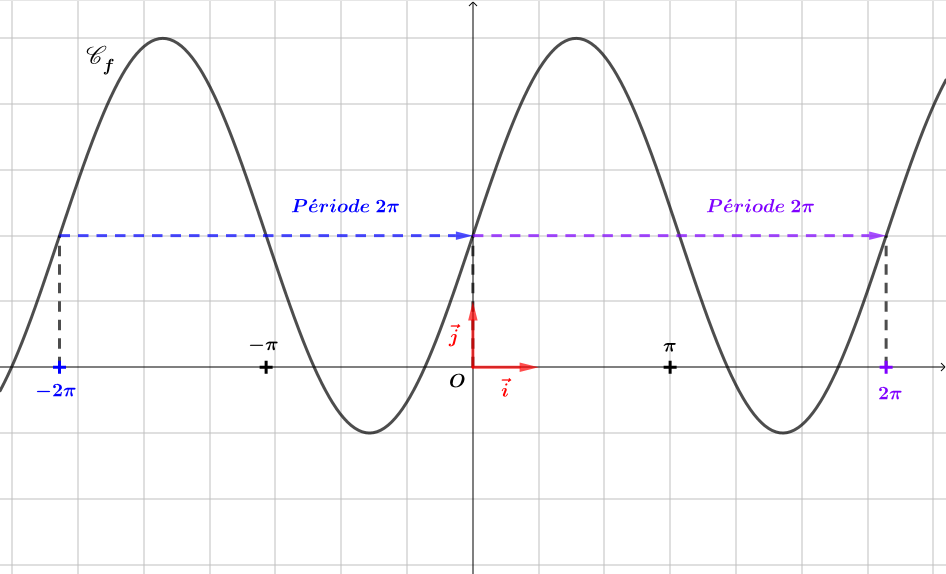
Soit f(x)=cos⁡2(x)−sin⁡2(x)f\left(x\right)=\cos ^{2} \left(x\right)-\sin ^{2} \left(x\right) . Montrer que ff est π−\pi -périodique.

Correction
  • ff est T−T-périodique si et seulement si f(x+T)=f(x)f\left(x+T\right)=f\left(x\right)
  • Les fonctions cosinus et sinus sont 2π−2\pi -périodique, c'est-à-dire cos⁡(x+2π)=cos⁡(x)\cos \left(x+2\pi \right)=\cos \left(x\right) et sin⁡(x+2π)=sin⁡(x)\sin \left(x+2\pi \right)=\sin \left(x\right)
    • f(x)=cos⁡2(x)−sin⁡2(x)f\left(x\right)=\cos ^{2} \left(x\right)-\sin ^{2} \left(x\right)
    f(x)=(cos⁡(x))2−(sin⁡(x))2f\left(x\right)=\left(\cos \left(x\right)\right)^{2} -\left(\sin \left(x\right)\right)^{2}
    f(x+π)=(cos⁡(x+π))2−(sin⁡(x+π))2f\left(x+\pi \right)=\left(\cos \left(x+\pi \right)\right)^{2} -\left(\sin \left(x+\pi \right)\right)^{2}
  • cos⁡(x+π)=−cos⁡(x)\cos \left(x+\pi \right)=-\cos \left(x\right)
  • sin⁡(x+π)=−sin⁡(x)\sin \left(x+\pi \right)=-\sin \left(x\right)
    • f(x+π)=(−cos⁡(x))2−(−sin⁡(x))2f\left(x+\pi \right)=\left(-\cos \left(x\right)\right)^{2} -\left(-\sin \left(x\right)\right)^{2}
    f(x+π)=(cos⁡(x))2−(sin⁡(x))2f\left(x+\pi \right)=\left(\cos \left(x\right)\right)^{2} -\left(\sin \left(x\right)\right)^{2}
    f(x+π)=cos⁡2(x)−sin⁡2(x)f\left(x+\pi \right)=\cos ^{2} \left(x\right)-\sin ^{2} \left(x\right)
    Il en résulte que
    f(x+π)=f(x)f\left(x+\pi \right)=f\left(x\right)
    donc ff est π−\pi -périodique.
    Question 2

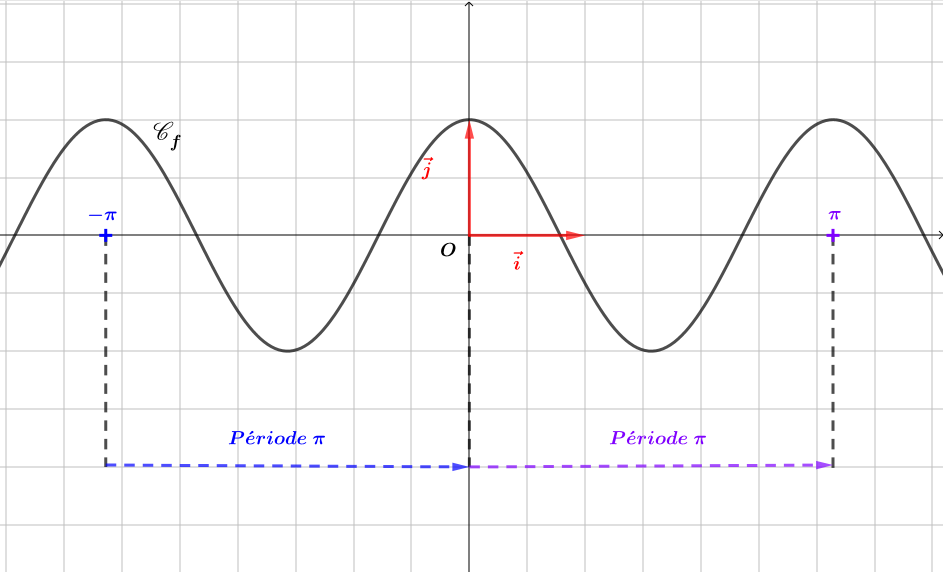
    Soit ff une fontion définie sur R\mathbb{R} par f(x)=2+3sin⁡(x)f\left(x\right)=2+3\sin \left(x\right). Montrer que ff est 2π−2\pi -périodique.

    Correction
  • ff est T−T-périodique si et seulement si f(x+T)=f(x)f\left(x+T\right)=f\left(x\right)
  • Les fonctions cosinus et sinus sont 2π−2\pi -périodique, c'est-à-dire cos⁡(x+2π)=cos⁡(x)\cos \left(x+2\pi \right)=\cos \left(x\right) et sin⁡(x+2π)=sin⁡(x)\sin \left(x+2\pi \right)=\sin \left(x\right)
    • f(x+2π)=2+3sin⁡(x+2π)f\left(x+2\pi \right)=2+3\sin \left(x+2\pi \right)
    f(x+2π)=2+3sin⁡(x)f\left(x+2\pi \right)=2+3\sin \left(x\right)
    Il en résulte que
    f(x+2π)=f(x)f\left(x+2\pi \right)=f\left(x\right)
    donc ff est 2π−2\pi -périodique.