Qui aura 20 en maths ?
💯 Teste ton niveau de maths et tente de gagner un des lots !S'inscrire au jeu →
Nouveau
🔥 Découvre nos fiches d'exercices gratuites avec corrections en vidéo !Accéder aux fiches →
Lecture graphique : nombre dérivé - Exercice 4
6 min
10
Question 1
A l'aide de la représentation graphique ci-dessous de la fonction :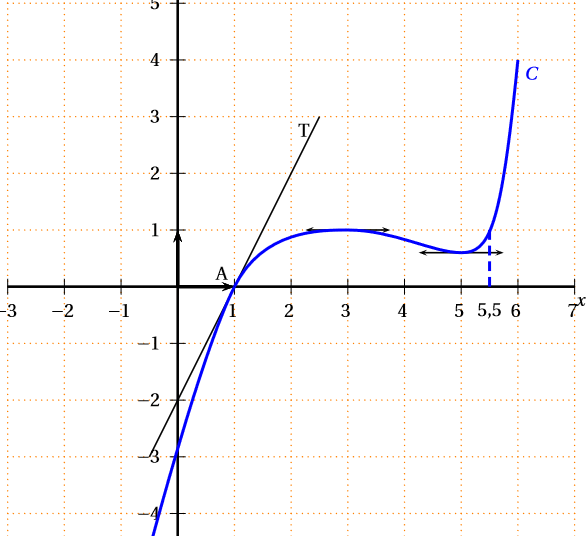 Donner les valeurs de :
Donner les valeurs de :

Correction
correspond au coefficient directeur de la tangente à la courbe au point d'abscisse .  Les points et appartiennent à cette tangente.
Les points et appartiennent à cette tangente.
A l'aide du point et du point on va pouvoir donner le coefficient directeur de la tangente.
Ainsi :

A l'aide du point et du point on va pouvoir donner le coefficient directeur de la tangente.
Ainsi :
Question 2
Correction
correspond au coefficient directeur de la tangente à la courbe au point d'abscisse .  La tangente est horizontale. Cela signifie que le coefficient directeur est nul.
La tangente est horizontale. Cela signifie que le coefficient directeur est nul.
Ainsi :

Ainsi :
Question 3
Correction
correspond au coefficient directeur de la tangente à la courbe au point d'abscisse .  La tangente est horizontale. Cela signifie que le coefficient directeur est nul.
La tangente est horizontale. Cela signifie que le coefficient directeur est nul.
Ainsi :

Ainsi :