Exercices types : $$3$$^ème partie - Exercice 1

Nous avons reproduit ci-dessous un rectangle dont la largeur vaut $$x$$ mètres et la longueur vaut $$x+2$$ mètres.
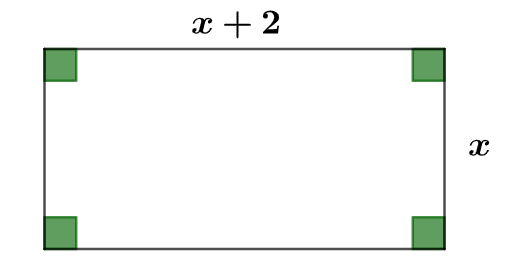L'aire d'un rectangle est donnée par la formule suivante : $$\text{longueur}\times \text{largeur}$$. Or , ici, nous savons que l'aire doit être égale à $$87,36$$ m$$^{2}$$. Il en résulte donc que :
$$\text{longueur}\times \text{largeur}=87,36$$ équivaut successivement à :
$$x\left(x+2\right)=87,36$$
$$x^{2} +2x-87,36=0$$. On reconnaît une équation trinôme du second degré.
Calcul du discriminant $$\Delta =b^{2} -4ac$$
Ainsi : $$\Delta =2^{2} -4\times 1\times \left(-87,36\right)$$
$$\Delta =353,44$$
Comme $$\Delta >0$$ alors l'équation admet deux racines réelles distinctes notées $$x{}_{1}$$ et $$x{}_{2}$$ telles que :
$$x{}_{1} =\frac{-b-\sqrt{\Delta } }{2a}$$ ainsi $$x{}_{1} =\frac{-2-\sqrt{353,44} }{2\times 1}$$ d'où $$x{}_{1} =-10,4$$
$$x{}_{2} =\frac{-b+\sqrt{\Delta } }{2a}$$ ainsi $$x{}_{2} =\frac{-2+\sqrt{353,44} }{2\times 1}$$ d'où $$x{}_{2} =8,4$$
Les racines de l'équation $$x^{2} +2x-87,36=0$$ sont donc :
Ici, rappelons que $$x$$ correspond à la largeur du rectangle. Dans ce cas, on rejette la valuer $$-10,4$$ car une distance ne peut pas être négative.
Dans ce cas, la largeur du rectangle sera de $$8,4$$ m et la longueur du rectangle sera de $$8,4+2=10,4$$ m.
Avec ces mesures, les dimensions $$8,4$$ et $$10,4$$, nous avons bien un rectangle dont l'aire vaut $$87,36$$ m$$^{2}$$.