Qui aura 20 en maths ?

💯 Teste ton niveau de maths et tente de gagner un des lots !S'inscrire au jeu  →

Nouveau

🔥 Découvre nos fiches d'exercices gratuites avec corrections en vidéo !Accéder aux fiches  →

Déterminer le signe d'une fonction sous forme factorisée - Exercice 2

12 min
25
Question 1
Dresser le tableau de signe de chacune des fonctions suivantes définies sur R\mathbb{R} .

f(x)=4(x−1)(2x−10)f\left(x\right)=4\left(x-1\right)\left(2x-10\right)

Correction

Pour étudier le signe d'un produit :
  • On étudie le signe de chaque facteur.
  • On regroupe dans un tableau le signe de chaque facteur. La première ligne du tableau contenant les valeurs, rangées dans l'ordre croissant, qui annulent chacun des facteurs.
  • On utilise la règle des signes pour remplir la dernière ligne
  •  D’une part :\red{\text{ D'une part :}}
    • x−1≥0⇔x≥1x-1\ge 0\Leftrightarrow x\ge1
    Cela signifie que l'on va mettre le signe ++ dans la ligne de x−1x-1 lorsque xx sera supérieur ou égale à 11.
  •  D’autre part :\red{\text{ D'autre part :}}
    • 2x−10≥0⇔2x≥10⇔x≥102⇔x≥52x-10\ge0\Leftrightarrow 2x\ge10\Leftrightarrow x\ge\frac{10}{2}\Leftrightarrow x\ge5
    Cela signifie que l'on va mettre le signe ++ dans la ligne de 2x−102x-10 lorsque xx sera supérieur ou égale à 55.
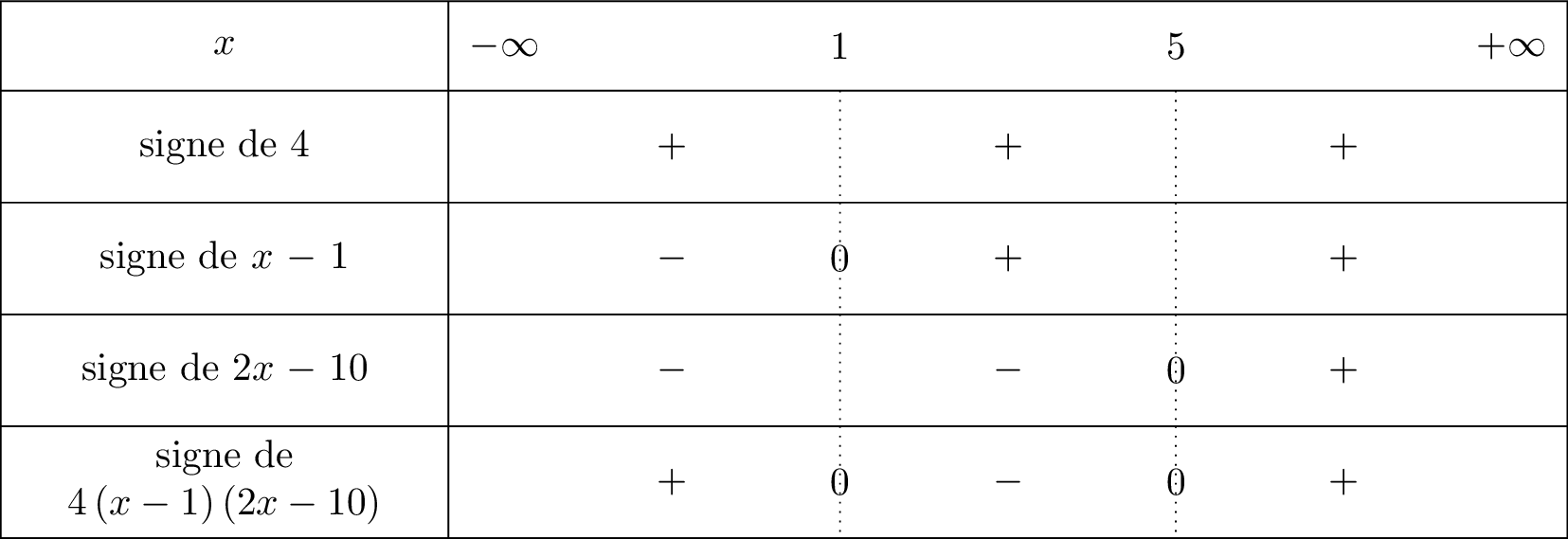
    Enfin, nous avons le nombre 4{\color{blue}4} devant dans l'expression f(x)=4(x−1)(2x−10)f\left(x\right)={\color{blue}4}\left(x-1\right)\left(2x-10\right). Nous allons mettre une ligne pour le nombre 4{\color{blue}4} et nous y intégrerons que des signes ++ car 4>04>0.
    Le tableau du signe de la fonction ff est donné ci-dessous :
    Question 2

    f(x)=−3(x+2)(x+6)f\left(x\right)=-3\left(x+2\right)\left(x+6\right)

    Correction

    Pour étudier le signe d'un produit :
    • On étudie le signe de chaque facteur.
    • On regroupe dans un tableau le signe de chaque facteur. La première ligne du tableau contenant les valeurs, rangées dans l'ordre croissant, qui annulent chacun des facteurs.
    • On utilise la règle des signes pour remplir la dernière ligne
  •  D’une part :\red{\text{ D'une part :}}
    • x+2≥0⇔x≥−2x+2\ge 0\Leftrightarrow x\ge-2
    Cela signifie que l'on va mettre le signe ++ dans la ligne de x+2x+2 lorsque xx sera supérieur ou égale à −2-2.
  •  D’autre part :\red{\text{ D'autre part :}}
    • x+6≥0⇔x≥−6x+6\ge0\Leftrightarrow x\ge-6
    Cela signifie que l'on va mettre le signe ++ dans la ligne de x+6x+6 lorsque xx sera supérieur ou égale à −6-6.
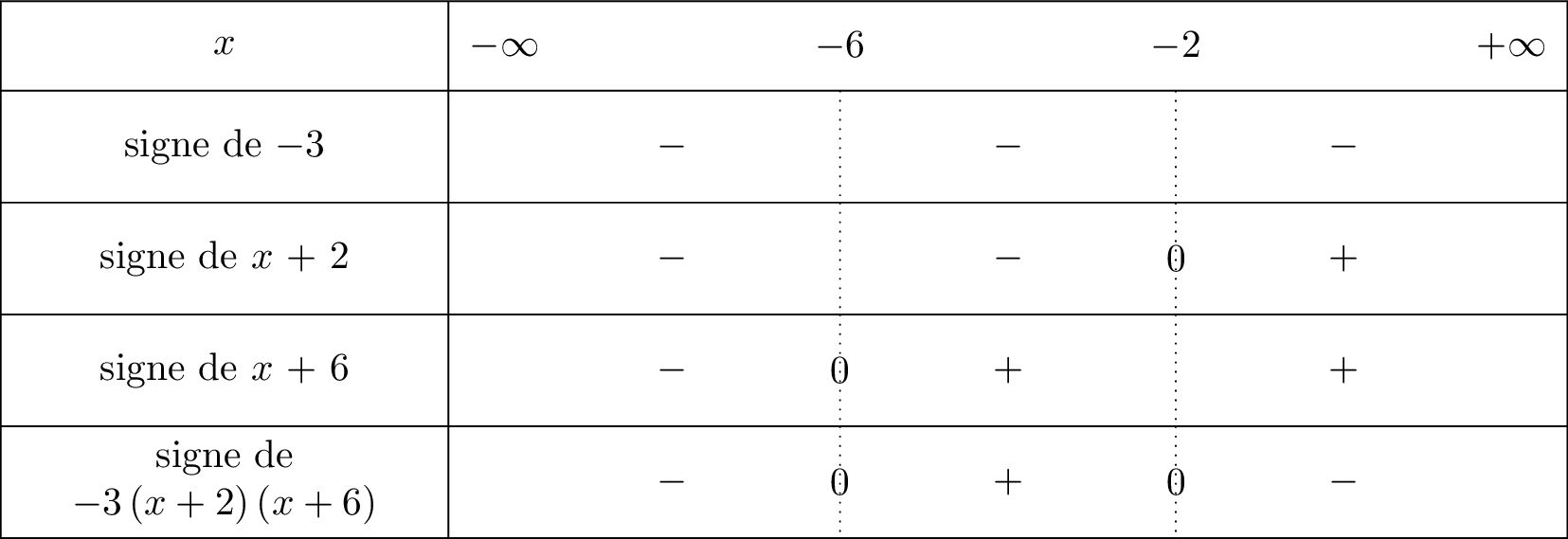
    Enfin, nous avons le nombre −3{\color{blue}-3} devant dans l'expression f(x)=−3(x+2)(x+6)f\left(x\right)={\color{blue}-3}\left(x+2\right)\left(x+6\right). Nous allons mettre une ligne pour le nombre −3{\color{blue}-3} et nous y intégrerons que des signes −- car −3<0-3<0.
    Le tableau du signe de la fonction ff est donné ci-dessous :
    Question 3

    f(x)=5(2x−8)(3−x)f\left(x\right)=5\left(2x-8\right)\left(3-x\right)

    Correction

    Pour étudier le signe d'un produit :
    • On étudie le signe de chaque facteur.
    • On regroupe dans un tableau le signe de chaque facteur. La première ligne du tableau contenant les valeurs, rangées dans l'ordre croissant, qui annulent chacun des facteurs.
    • On utilise la règle des signes pour remplir la dernière ligne
  •  D’une part :\red{\text{ D'une part :}}
    • 2x−8≥0⇔2x≥8⇔x≥82⇔x≥42x-8\ge 0\Leftrightarrow 2x\ge8\Leftrightarrow x\ge \frac{8}{2} \Leftrightarrow x\ge 4
    Cela signifie que l'on va mettre le signe ++ dans la ligne de 2x−82x-8 lorsque xx sera supérieur ou égale à 44.
  •  D’autre part :\red{\text{ D'autre part :}}
    • 3−x≥0⇔−x≥−3⇔x≤−3−1⇔x≤33-x\ge 0\Leftrightarrow -x\ge -3\Leftrightarrow x\le \frac{-3}{-1} \Leftrightarrow x\le 3
    Cela signifie que l'on va mettre le signe ++ dans la ligne de 3−x3-x lorsque xx sera inférieur ou égale à 33.
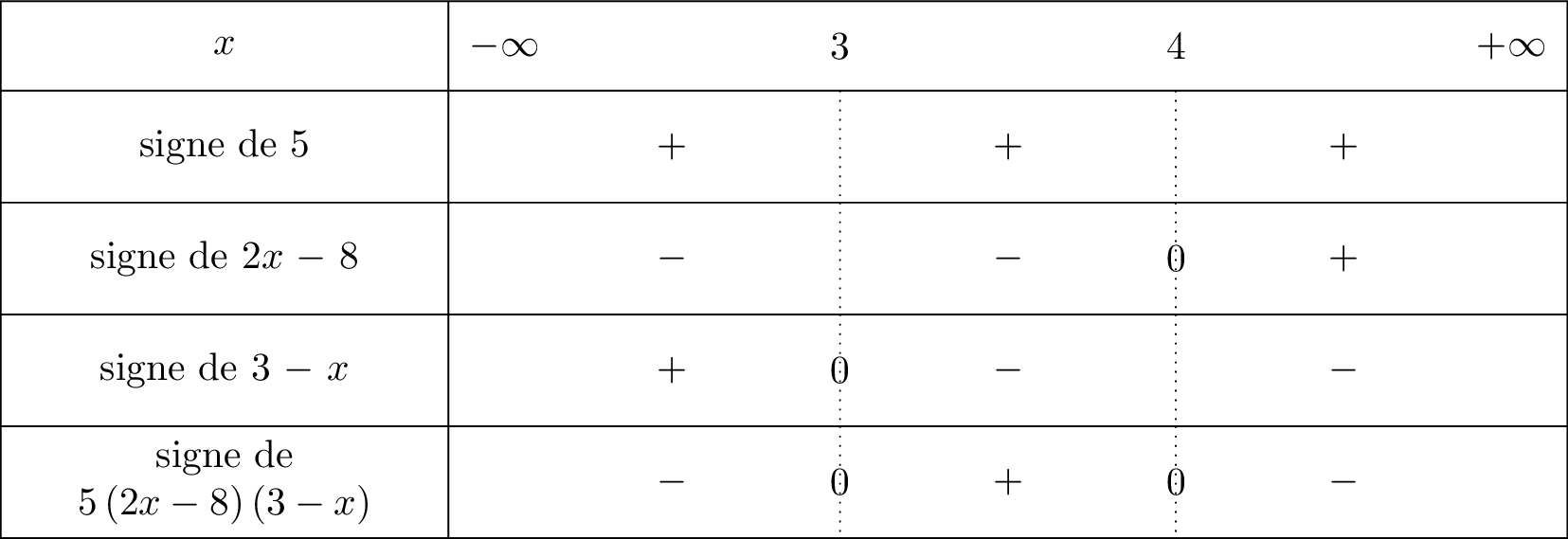
    Enfin, nous avons le nombre 5{\color{blue}5} devant dans l'expression f(x)=5(2x−8)(3−x)f\left(x\right)={\color{blue}5}\left(2x-8\right)\left(3-x\right). Nous allons mettre une ligne pour le nombre 5{\color{blue}5} et nous y intégrerons que des signes ++ car 5>05>0.
    Le tableau du signe de la fonction ff est donné ci-dessous :