Qui aura 20 en maths ?
💯 Teste ton niveau de maths et tente de gagner un des lots !S'inscrire au jeu →
Nouveau
🔥 Découvre nos fiches d'exercices gratuites avec corrections en vidéo !Accéder aux fiches →
Comment étudier l'ensemble des points vérifiant la relation - Exercice 1
5 min
10
Question 1
Soient et deux points du plan tels que .
Déterminer l'ensemble des points du plan vérifiant .
Correction
Soit le milieu du segment . On applique la formule de la médiane .
Comme et que on a alors :
équivaut successivement à :
car correspond à une distance donc
L'ensemble des points vérifiant est le cercle de centre et de rayon .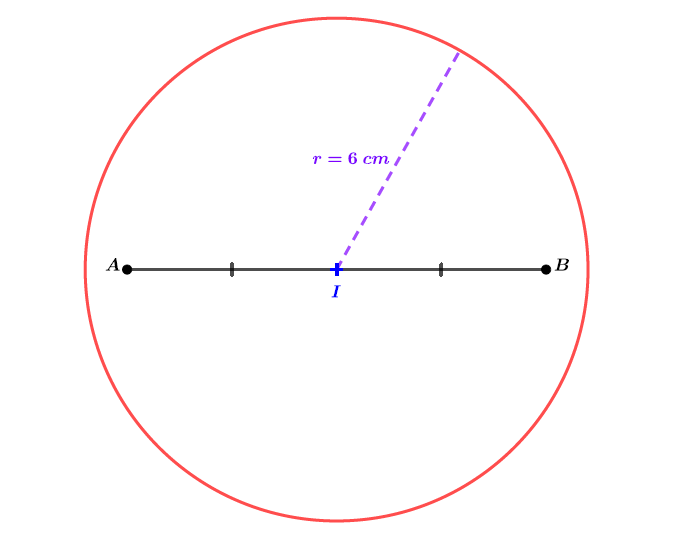
- Formule de la médiane
- Pour tout point du plan, on a : où est le milieu du segment
équivaut successivement à :
car correspond à une distance donc
L'ensemble des points vérifiant est le cercle de centre et de rayon .
