Nouveau
🤔 Bloqué sur un exercice ou une notion de cours ? Échange avec un prof sur le tchat !Découvrir →
Arbres pondérés et formule des probabilités totales : pour se perfectionner - Exercice 2
8 min
15
Question 1
Soit l'arbre pondéré suivant :
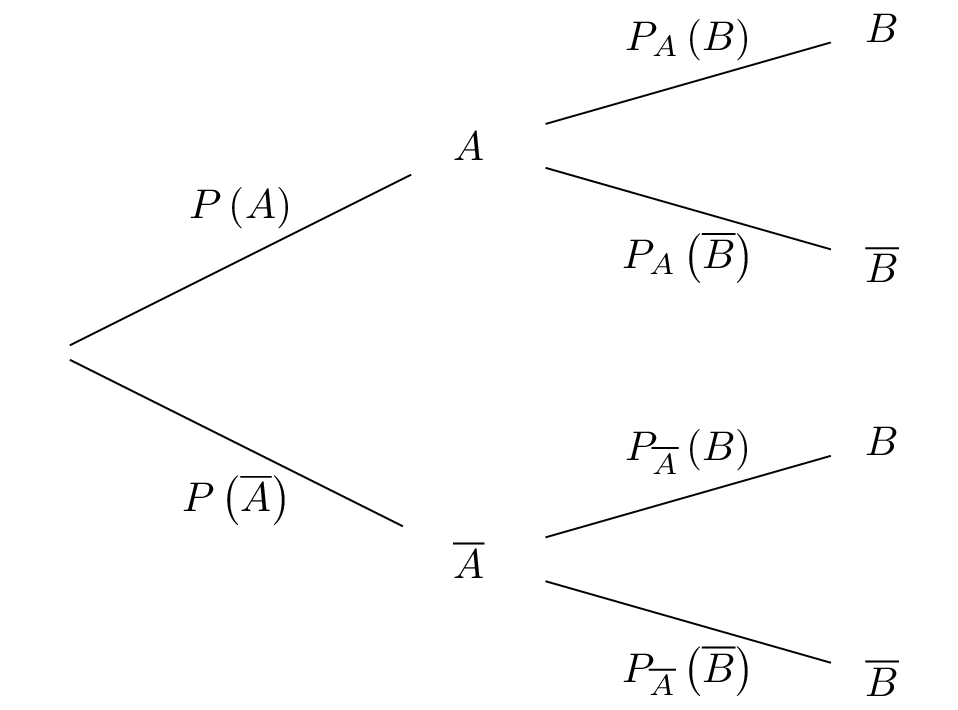

Soient et , tels que et et
Calculez ?
Calculez ?
Correction
On remplit l'arbre pondéré grâce aux informations données par l'énoncé.
En noirs les valeurs de l'énoncé et en rouge les valeurs que l'on déduit.
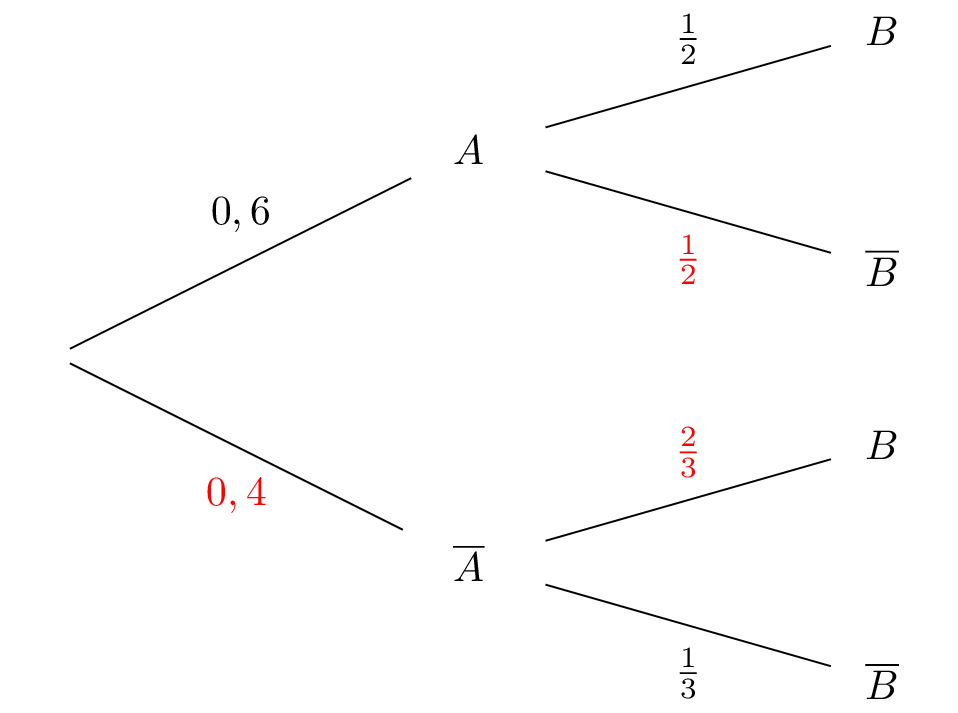 et forment une partition de l'univers.
et forment une partition de l'univers.
D'après la formule des probabilités totales on a :
Soit :
Ainsi :
En noirs les valeurs de l'énoncé et en rouge les valeurs que l'on déduit.

D'après la formule des probabilités totales on a :
Soit :
Ainsi :