Qui aura 20 en maths ?
💯 Teste ton niveau de maths et tente de gagner un des lots !S'inscrire au jeu →
Nouveau
🔥 Découvre nos fiches d'exercices gratuites avec corrections en vidéo !Accéder aux fiches →
Vérifions si nous sommes prêt pour le jour du contrôle - Exercice 1
15 min
25
Soit un entier naturel.
Soit la suite définie par
Soit la suite définie par
Question 1
Indiquer si la suite est définie par une formule explicite ou bien par récurrence.
Correction
est une suite définie par une formule . En effet, est exprimé en fonction de .
Question 2
Calculer .
Correction
Ainsi :
Question 3
Calculer le septième terme de la suite .
Correction
Ici il faut être vigilant, le septième terme de la suite ne correspond pas à .
En effet, le premier terme de la suite est ce qui permet d'affirmer que le septième terme de la suite est .
Ainsi :
Ainsi :
En effet, le premier terme de la suite est ce qui permet d'affirmer que le septième terme de la suite est .
Ainsi :
Ainsi :
Question 4
Etudier le sens de variation de la suite .
Correction
- Si alors la suite est croissante.
- Si alors la suite est décroissante.
- Si alors la suite est constante.
Comme alors :
2ème étape : Calcul de puis étude du signe de .
Or alors la suite est
Question 5
Conjecturer la limite de la suite .
Correction
Pour conjecturer une limite, il faut calculer les termes pour des valeurs grandes de . Dans notre exemple, nous avons calculer et .
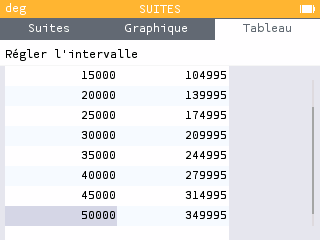 On remarque que les termes de la suite de rang élevé de plus en plus .
On remarque que les termes de la suite de rang élevé de plus en plus .
On conjecture donc que la suite a pour limite .
On peut également dire que la suite est une suite .
Nous écrivons alors que :
Ci-dessous, on observe que la représentation graphique de la suite ne cesse d'augmenter et les valeurs augmentent vers .
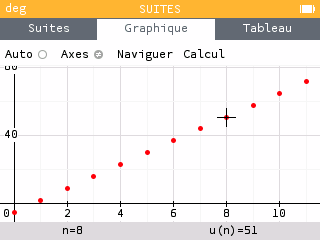

On conjecture donc que la suite a pour limite .
On peut également dire que la suite est une suite .
Nous écrivons alors que :
Ci-dessous, on observe que la représentation graphique de la suite ne cesse d'augmenter et les valeurs augmentent vers .
