Nouveau
🔥 Découvre nos fiches d'exercices gratuites avec corrections en vidéo !Accéder aux fiches →
Tchat avec un prof
🤔 Bloqué sur un exercice ou une notion de cours ? Échange avec un prof sur le tchat !Découvrir →
Vecteurs colinéaires - Exercice 3
10 min
20
Dans chacun des cas suivants, dire si les droites et sont parallèles.
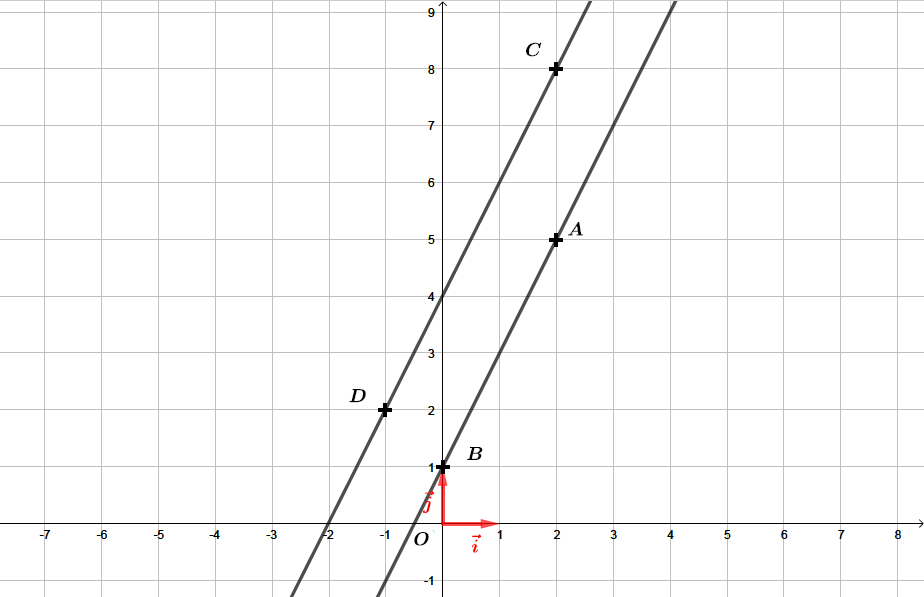
Question 1
Soient les points : , , et
Correction
Les droites et sont parallèles si les vecteurs et sont colinéaires.
d'où : d'où
Or : .
Les vecteurs et sont colinéaires.
Les droites et sont parallèles.
Question 2
Soient les points : , , .
Déterminer les coordonnées du point ( Sachant que le point appartient à l'axe des abscisses), tel que les droites et soient parallèles.
Correction
On sait que le point appartient à l'axe des abscisses, il en résulte donc que .
Calculons maintenant les vecteurs et
d'où
d'où
Les droites et sont parallèles.
Les vecteurs et sont donc colinéaires. Ainsi :
Les coordonnées du point sont alors :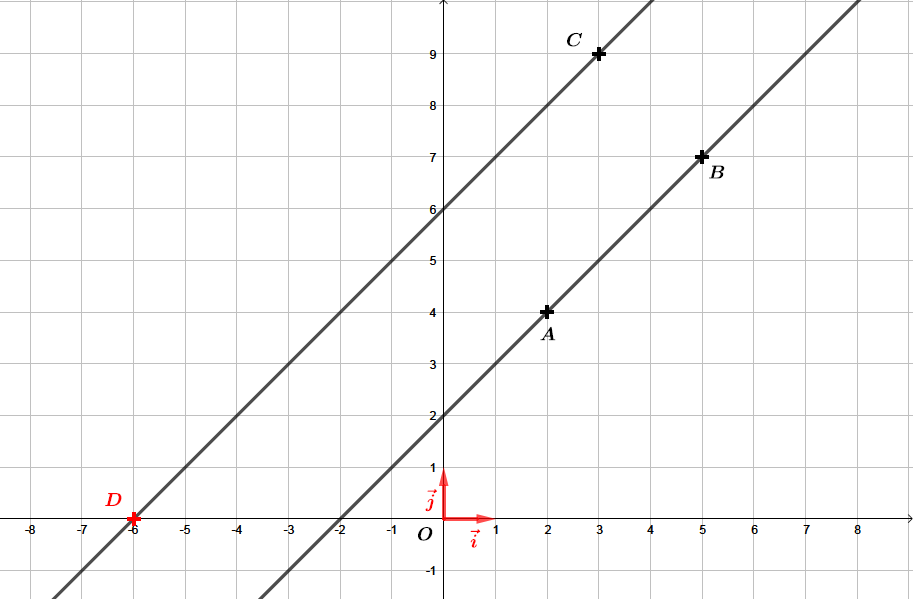
Calculons maintenant les vecteurs et
d'où
d'où
Les droites et sont parallèles.
Les vecteurs et sont donc colinéaires. Ainsi :
Les coordonnées du point sont alors :

Signaler une erreur
Aide-nous à améliorer nos contenus en signalant les erreurs ou problèmes que tu penses avoir trouvés.
Connecte-toi ou crée un compte pour signaler une erreur.