Qui aura 20 en maths ?
💯 Le grand concours 100% Terminale revient le 31 janvier 2026 à l'ESIEA Paris !Découvrir →
Nouveau
🔥 Découvre nos fiches d'exercices gratuites avec corrections en vidéo !Accéder aux fiches →
Exercices types : ème partie - Exercice 3
20 min
35
On se place dans le repère orthonormal . On considère deux points et et la droite d'équation cartésienne : 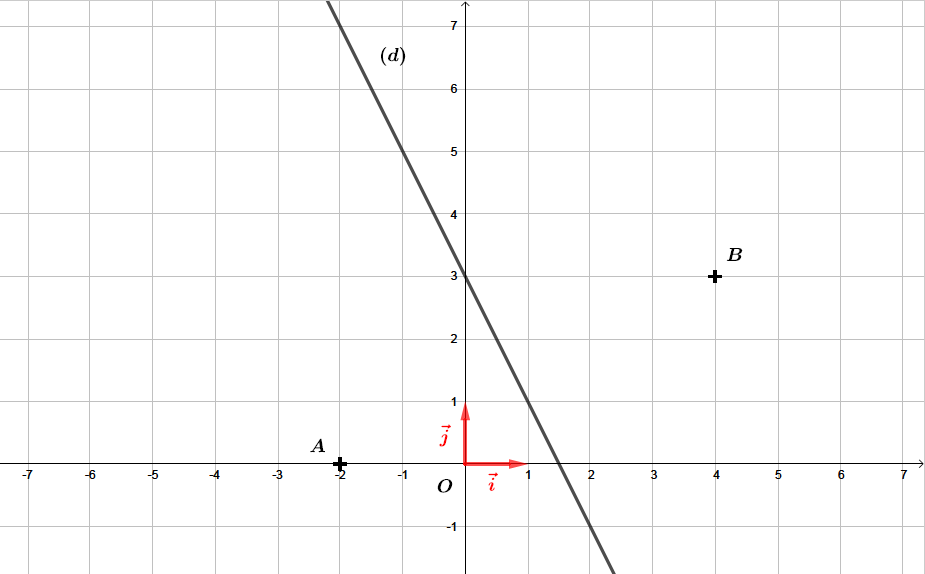

Question 1
Déterminer une équation cartésienne de la droite .
Correction
Nous allons calculer le vecteur qui sera un vecteur directeur de la droite .
d'où
étant un vecteur directeur de , on en déduit que : et .
Ainsi , on a : .
Or le point appartient à la droite , donc les coordonnées du point vérifie .
Il vient alors que :
Finalement, l'équation cartésienne de la droite est : que l'on peut aussi écrire .
d'où
étant un vecteur directeur de , on en déduit que : et .
Ainsi , on a : .
Or le point appartient à la droite , donc les coordonnées du point vérifie .
Il vient alors que :
Finalement, l'équation cartésienne de la droite est : que l'on peut aussi écrire .
Question 2
Montrer que les droites et sont sécantes.
Correction
Deux droites et sont sécantes si leurs vecteurs directeurs respectifs ne sont pas colinéaires.
Soit un vecteur de la droite .Soit un vecteur de la droite .
Le vecteurs et ne sont pas colinéaires car : .
Les droites et ne sont donc pas parallèles, elles sont donc sécantes.
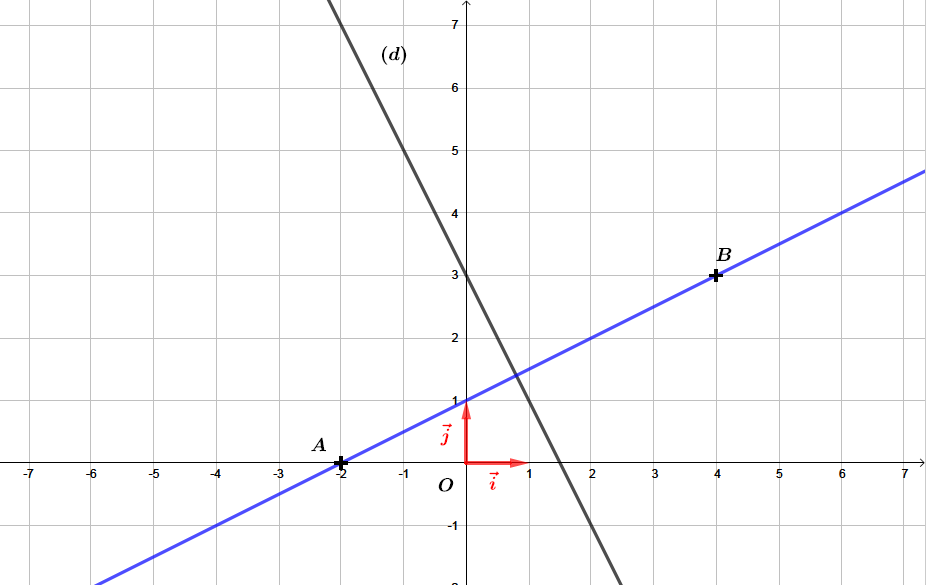
Question 3
Déterminer les coordonnées du point , intersection des droites et .
Correction
. Nous allons résoudre le système à l'aide de la méthode de la combinaison. On va multiplier la première ligne par et la deuxième ligne par afin que les coefficients devant les soient opposées. Il vient alors que :
. Nous allons maintenant additionner les deux lignes. Pour cela nous réécrivons un système, la première ligne sera la première équation du système initial et la deuxième ligne l'addition des deux lignes du système précédent.
. Maintenant, la deuxième ligne est une équation à une inconnue que nous allons résoudre :
Les coordonnées du point d'intersection entre les droites et est le point de coordonnées .
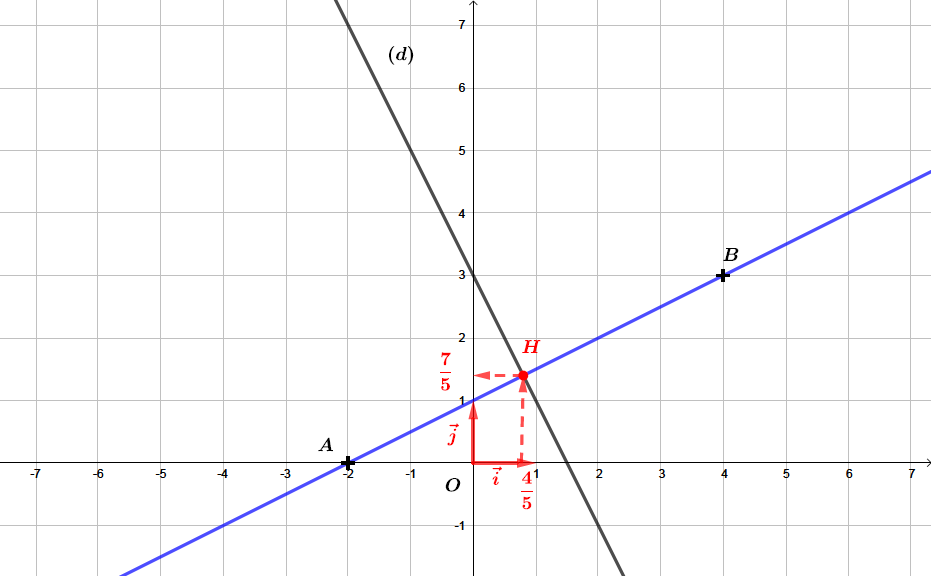
Question 4
Soit le point .
Le point appartient-il à ?
Le point appartient-il à ?
Correction
Le point appartient à l'équation cartésienne si les coordonnées de vérifient l'équation.
Autrement dit, il faut que .
Il vient alors que :
Il en résulte que le point appartient bien à la droite .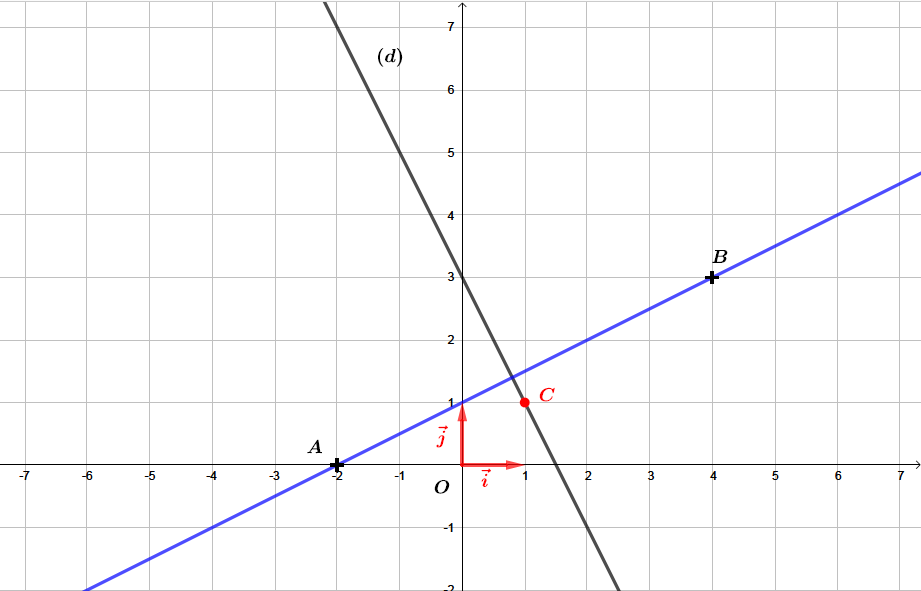
Autrement dit, il faut que .
Il vient alors que :
Il en résulte que le point appartient bien à la droite .

Signaler une erreur
Aide-nous à améliorer nos contenus en signalant les erreurs ou problèmes que tu penses avoir trouvés.
Connecte-toi ou crée un compte pour signaler une erreur.