Nouveau
🤔 Bloqué sur un exercice ou une notion de cours ? Échange avec un prof sur le tchat !Découvrir →
Simplification d'expressions en cosinus et en sinus - Exercice 1
12 min
25
Question 1
Simplifier aux maximum les expressions suivantes :
.
Correction
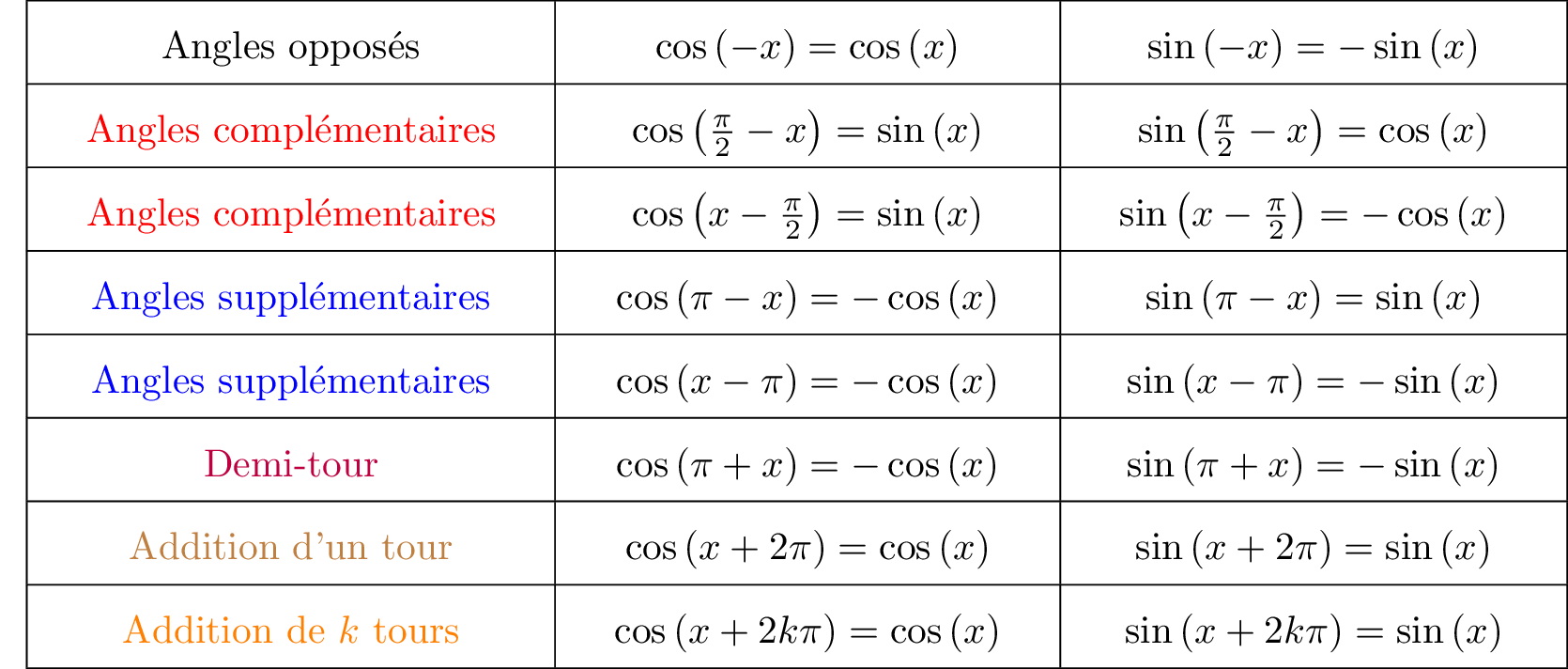
D'où :
Question 2
.
Correction
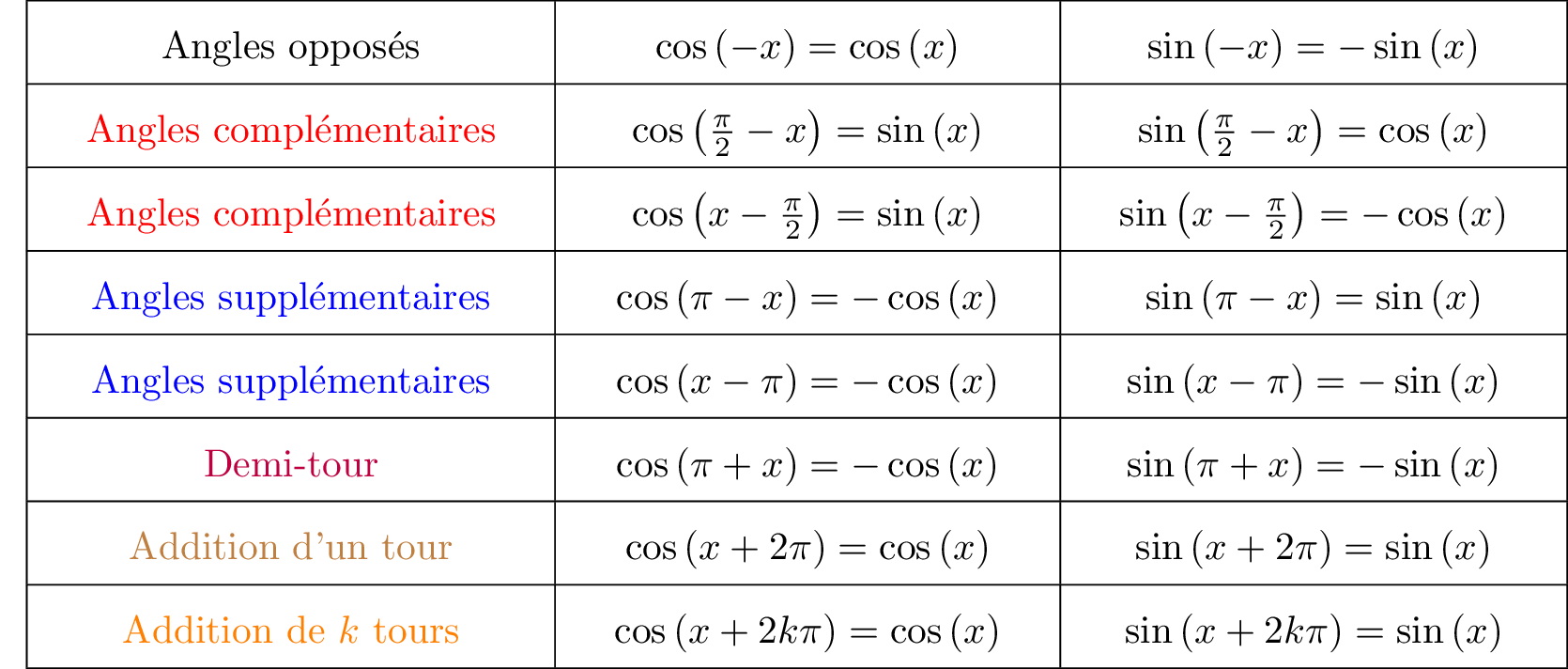
Ainsi :
Question 3
.
Correction
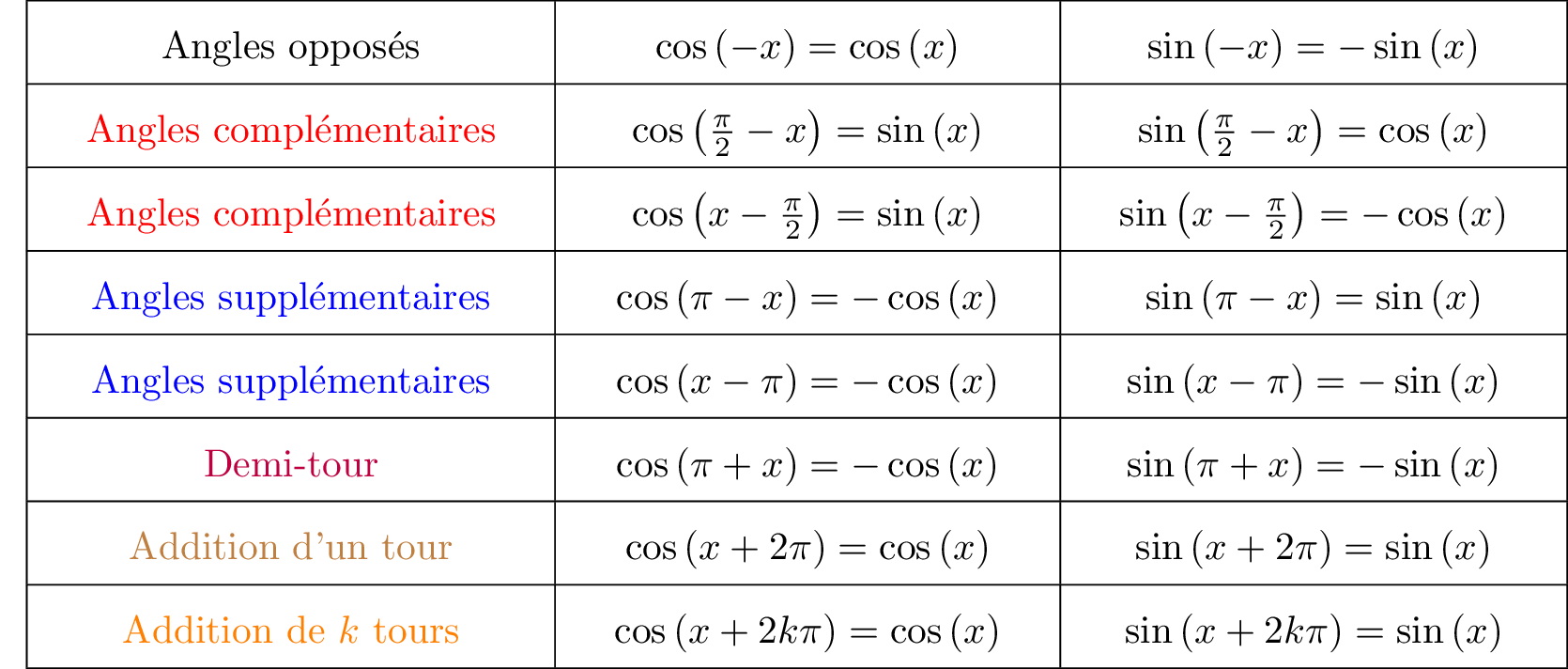
Finalement :
Question 4
.
Correction
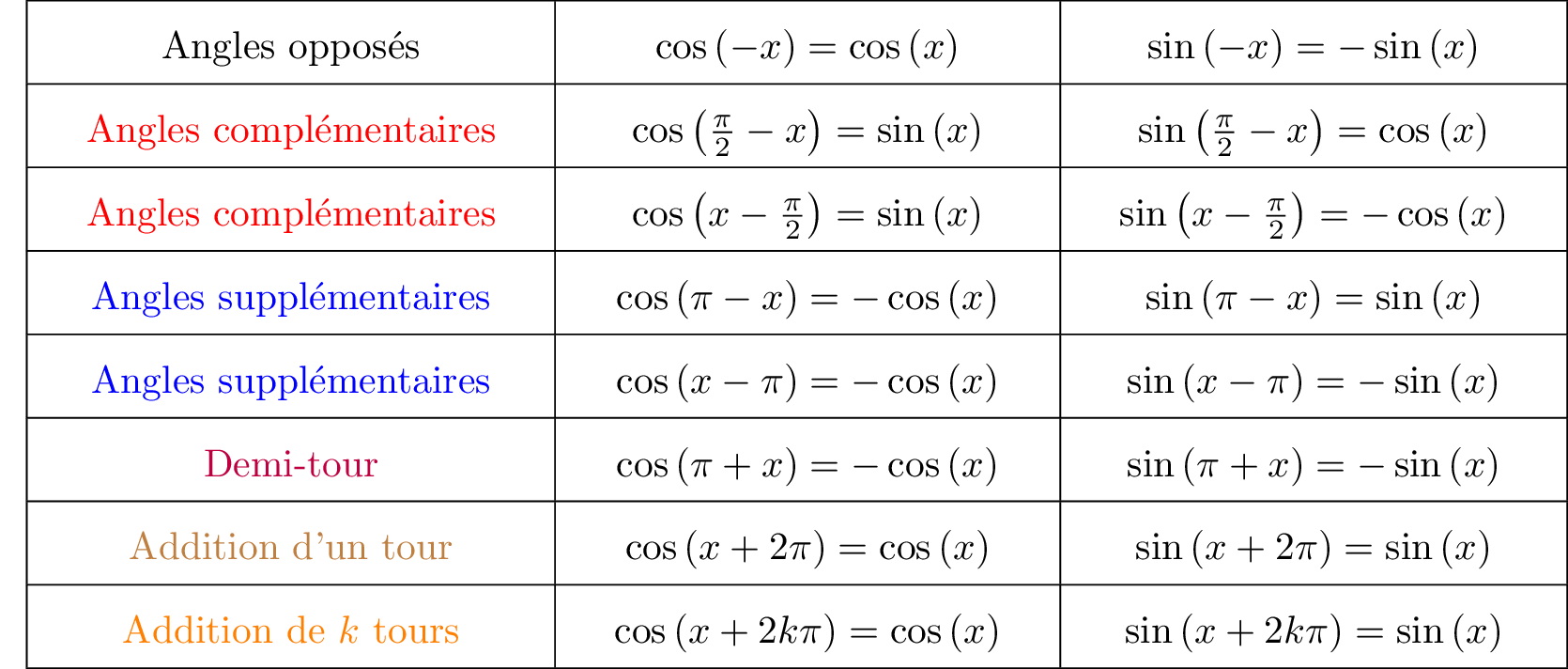
Finalement :