Nouveau

🤔 Bloqué sur un exercice ou une notion de cours ? Échange avec un prof sur le tchat !Découvrir  →

Sous forme de petits problèmes - Exercice 3

20 min
40
ABCABC est un triangle rectangle isocèle en BB de sens direct. Les triangles ANBANB et AMCAMC sont équilatéraux, orientés dans le sens direct.
La représentation graphique de ces trois éléments est donnée ci-dessous:
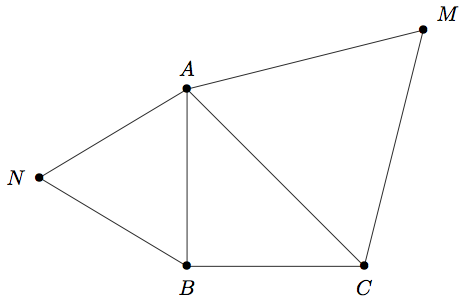Déterminer la mesure principale des angles orientés suivants :
Question 1

(BC→;AC→)\left(\overrightarrow{BC} ;\overrightarrow{AC} \right)

Correction
Soient les vecteurs u→\overrightarrow{u} et v→\overrightarrow{v} on a alors :
(−u→;−v→)=(u→;v→)\left(-\overrightarrow{u} ;-\overrightarrow{v} \right)=\left(\overrightarrow{u} ;\overrightarrow{v} \right)
On a :
(BC→;AC→)=(−CB→;−CA→)\left(\overrightarrow{BC} ;\overrightarrow{AC} \right)=\left(-\overrightarrow{CB} ;-\overrightarrow{CA} \right)
(BC→;AC→)=(CB→;CA→)\left(\overrightarrow{BC} ;\overrightarrow{AC} \right)=\left(\overrightarrow{CB} ;\overrightarrow{CA} \right) . Ici l'angle orienté (CB→;CB→)\left(\overrightarrow{CB} ;\overrightarrow{CB} \right) est dans le sens indirect.
(BC→;AC→)=−π4\left(\overrightarrow{BC} ;\overrightarrow{AC} \right)=-\frac{\pi }{4}

Question 2

(AN→;AC→)\left(\overrightarrow{AN} ;\overrightarrow{AC} \right)

Correction
Soient les vecteurs u→\overrightarrow{u} , v→\overrightarrow{v} et w→\overrightarrow{w} on a alors : (u→;v→)+(v→;w→)=(u→;w→)\left(\overrightarrow{u} ;\overrightarrow{v} \right)+\left(\overrightarrow{v} ;\overrightarrow{w} \right)=\left(\overrightarrow{u} ;\overrightarrow{w} \right).
Il s'agit de la relation de Chasles.
D'après la relation de Chasles, on a :
(AN→;AC→)=(AN→;AB→)+(AB→;AC→)\left(\overrightarrow{AN} ;\overrightarrow{AC} \right)=\left(\overrightarrow{AN} ;\overrightarrow{AB} \right)+\left(\overrightarrow{AB} ;\overrightarrow{AC} \right) . Ici les angles orientés (AN⃗;AB⃗)\left(\vec{AN} ;\vec{AB} \right) et (AN→;AB→)\left(\overrightarrow{AN} ;\overrightarrow{AB} \right) sont dans le sens direct.
(AN→;AC→)=π4+π3\left(\overrightarrow{AN} ;\overrightarrow{AC} \right)=\frac{\pi }{4}+\frac{\pi }{3}
Ainsi :
(AN→;AC→)=7π12\left(\overrightarrow{AN} ;\overrightarrow{AC} \right)=\frac{7\pi }{12}
Question 3

(MA→;AB→)\left(\overrightarrow{MA} ;\overrightarrow{AB} \right)

Correction
Soient les vecteurs u→\overrightarrow{u} et v→\overrightarrow{v} on a alors :
(−u→;v→)=(u→;v→)+π\left(-\overrightarrow{u} ;\overrightarrow{v} \right)=\left(\overrightarrow{u} ;\overrightarrow{v} \right)+\pi
On a :
(MA→;AB→)=(−AM→;AB→)\left(\overrightarrow{MA} ;\overrightarrow{AB} \right)=\left(-\overrightarrow{AM} ;\overrightarrow{AB} \right)
(MA→;AB→)=(AM→;AB→)+π\left(\overrightarrow{MA} ;\overrightarrow{AB} \right)=\left(\overrightarrow{AM} ;\overrightarrow{AB} \right)+\pi
(MA→;AB→)=(AM→;AB→)+π\left(\overrightarrow{MA} ;\overrightarrow{AB} \right)=\left(\overrightarrow{AM} ;\overrightarrow{AB} \right)+\pi
(MA→;AB→)=(AM→;AC→)+(AC→;AB→)+π\left(\overrightarrow{MA} ;\overrightarrow{AB} \right)=\left(\overrightarrow{AM} ;\overrightarrow{AC}\right)+\left(\overrightarrow{AC} ;\overrightarrow{AB} \right)+\pi . On a utilisé la relation de Chasles.
Les angles orientés (AM→;AC→)\left(\overrightarrow{AM} ;\overrightarrow{AC}\right) et (AC→;AB→)\left(\overrightarrow{AC} ;\overrightarrow{AB}\right) sont dans le sens indirect.
Ainsi :
(MA→;AB→)=−π3+−π4+π\left(\overrightarrow{MA} ;\overrightarrow{AB} \right)=\frac{-\pi }{3} + \frac{-\pi }{4} +\pi
(MA→;AB→)=5π12\left(\overrightarrow{MA} ;\overrightarrow{AB} \right)=\frac{5\pi }{12}
Question 4

(AN→;AM→)\left(\overrightarrow{AN} ;\overrightarrow{AM} \right)

Correction
Soient les vecteurs u→\overrightarrow{u} , v→\overrightarrow{v} et w→\overrightarrow{w} on a alors : (u→;v→)+(v→;w→)=(u→;w→)\left(\overrightarrow{u} ;\overrightarrow{v} \right)+\left(\overrightarrow{v} ;\overrightarrow{w} \right)=\left(\overrightarrow{u} ;\overrightarrow{w} \right).
Il s'agit de la relation de Chasles.
D'après la relation de Chasles, on a :
(AN→;AM→)=(AN→;AB→)+(AB→;AC→)+(AC→;AM→)\left(\overrightarrow{AN} ;\overrightarrow{AM} \right)=\left(\overrightarrow{AN} ;\overrightarrow{AB} \right)+\left(\overrightarrow{AB} ;\overrightarrow{AC} \right)+\left(\overrightarrow{AC} ;\overrightarrow{AM} \right)
Les angles orientés (AN→;AB→) \left(\overrightarrow{AN} ;\overrightarrow{AB} \right) ; (AB→;AC→)\left(\overrightarrow{AB} ;\overrightarrow{AC} \right) et (AC→;AM→)\left(\overrightarrow{AC} ;\overrightarrow{AM} \right) sont dans le sens direct. Il vient alors que :
(AN→;AM→)=π3+π4+π3\left(\overrightarrow{AN} ;\overrightarrow{AM} \right)=\frac{\pi }{3} +\frac{\pi }{4} +\frac{\pi }{3}
(AN→;AM→)=11π12\left(\overrightarrow{AN} ;\overrightarrow{AM} \right)=\frac{11\pi }{12}
Ainsi :
(AN→;AM→)=11π12\left(\overrightarrow{AN} ;\overrightarrow{AM} \right)=\frac{11\pi }{12}

Question 5

(AM→;CB→)\left(\overrightarrow{AM} ;\overrightarrow{CB} \right)

Correction
Soient les vecteurs u→\overrightarrow{u} , v→\overrightarrow{v} et w→\overrightarrow{w} on a alors : (u→;v→)+(v→;w→)=(u→;w→)\left(\overrightarrow{u} ;\overrightarrow{v} \right)+\left(\overrightarrow{v} ;\overrightarrow{w} \right)=\left(\overrightarrow{u} ;\overrightarrow{w} \right).
Il s'agit de la relation de Chasles.
D'après la relation de Chasles, on a :
(AM→;CB→)=(AM→;AC→)+(AC→;CB→)\left(\overrightarrow{AM} ;\overrightarrow{CB} \right)=\left(\overrightarrow{AM} ;\overrightarrow{AC} \right)+\left(\overrightarrow{AC} ;\overrightarrow{CB} \right)
(AM→;CB→)=(AM→;AC→)+(−CA→;CB→)\left(\overrightarrow{AM} ;\overrightarrow{CB} \right)=\left(\overrightarrow{AM} ;\overrightarrow{AC} \right)+\left(-\overrightarrow{CA} ;\overrightarrow{CB} \right)
Soient les vecteurs u→\overrightarrow{u} et v→\overrightarrow{v} on a alors :
(−u→;v→)=(u→;v→)+π\left(-\overrightarrow{u} ;\overrightarrow{v} \right)=\left(\overrightarrow{u} ;\overrightarrow{v} \right)+\pi
(AM→;CB→)=(AM→;AC→)+(CA→;CB→)+π\left(\overrightarrow{AM} ;\overrightarrow{CB} \right)=\left(\overrightarrow{AM} ;\overrightarrow{AC} \right)+\left(\overrightarrow{CA} ;\overrightarrow{CB} \right)+\pi
(AM→;CB→)=−π3+π4+π=\left(\overrightarrow{AM} ;\overrightarrow{CB} \right)=\frac{-\pi }{3} +\frac{\pi }{4}+ \pi=. L'angle orienté (AM→;AC→)\left(\overrightarrow{AM} ;\overrightarrow{AC} \right) est dans le sens indirect et l'angle orienté (CA→;CB→)\left(\overrightarrow{CA} ;\overrightarrow{CB} \right) est dans le sens direct.
Ainsi :
(AM→;CB→)=11π12\left(\overrightarrow{AM} ;\overrightarrow{CB} \right)=\frac{11\pi }{12}

Signaler une erreur

Aide-nous à améliorer nos contenus en signalant les erreurs ou problèmes que tu penses avoir trouvés.

Connecte-toi ou crée un compte pour signaler une erreur.