Qui aura 20 en maths ?
💯 Le grand concours 100% Terminale revient le 31 janvier 2026 à l'ESIEA Paris !Découvrir →
Nouveau
🔥 Découvre nos fiches d'exercices gratuites avec corrections en vidéo !Accéder aux fiches →
Sous forme de petits problèmes - Exercice 2
25 min
45
est un carré et un triangle équilatéral, orientés dans le sens direct, dont les représentations graphiques sont données ci-dessous:
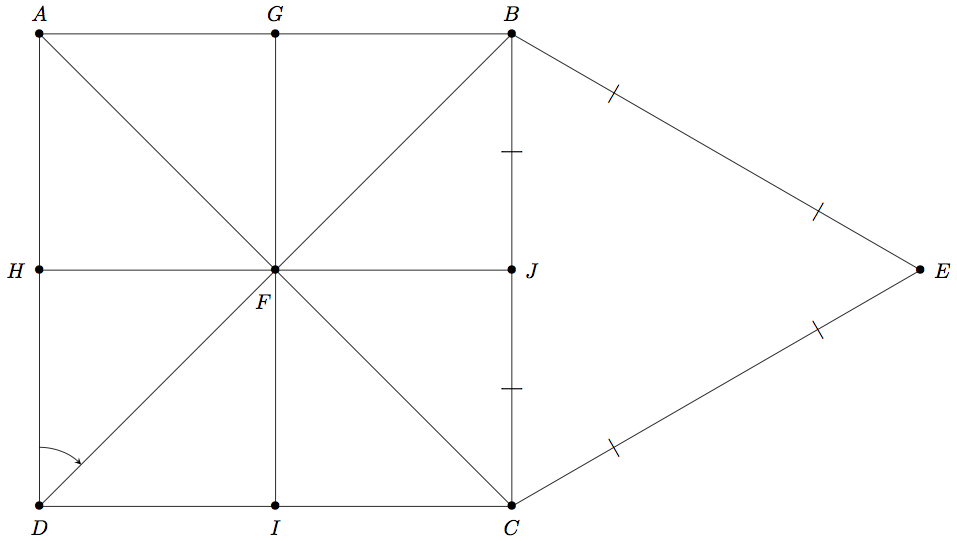 Déterminer la mesure principale des angles orientés suivants :
Déterminer la mesure principale des angles orientés suivants :

Question 1
Correction
Les vecteurs et sont égaux. On peut donc écrire que :
. Or les vecteurs et ont la même origine, on peut lire alors que :
. Or les vecteurs et ont la même origine, on peut lire alors que :
. Ici l'angle est dans le sens indirect.
Question 2
Correction
Soient les vecteurs et on a alors :
Les vecteurs et sont égaux. On peut donc écrire que :. On a utilisé le rappel. Ici l'angle orienté est dans le sens direct.
. Ce n'est pas une mesure principale, on va donc retrancher .
Ainsi :
.
Question 3
Correction
Soient deux vecteurs et .
Les vecteurs et sont colinéaires et de même sens. Ainsi : - Si les vecteurs et sont colinéaires et de même sens alors l'angle orienté
- Si les vecteurs et sont colinéaires et de sens opposés alors l'angle orienté
.
Question 4
Correction
Soient deux vecteurs et .
Les vecteurs et sont colinéaires et de sens opposés. Ainsi : - Si les vecteurs et sont colinéaires et de même sens alors l'angle orienté
- Si les vecteurs et sont colinéaires et de sens opposés alors l'angle orienté
.
Question 5
Correction
Soient les vecteurs et on a alors :
On a :. Ici l'angle est dans le sens indirect.
Ainsi :
.
Question 6
Correction
Soient les vecteurs et on a alors :
On a :. Ici l'angle est dans le sens indirect.
Ainsi :
.
Question 7
Correction
Soient les vecteurs , et on a alors : .
Il s'agit de la relation de Chasles.
A l'aide de la relation de Chasles, on peut écrire que :Il s'agit de la relation de Chasles.
Or, d'après la représentation graphique, on peut lire que :
De plus :
Et enfin :
Il en résulte que :
. Ce n'est pas une mesure principale, on va retrancher , cela nous donne donc :
.
Signaler une erreur
Aide-nous à améliorer nos contenus en signalant les erreurs ou problèmes que tu penses avoir trouvés.
Connecte-toi ou crée un compte pour signaler une erreur.