Nouveau
🤔 Bloqué sur un exercice ou une notion de cours ? Échange avec un prof sur le tchat !Découvrir →
Exercices types : ère partie - Exercice 3
20 min
40
Ci-dessous, on a construit une ligne brisée .
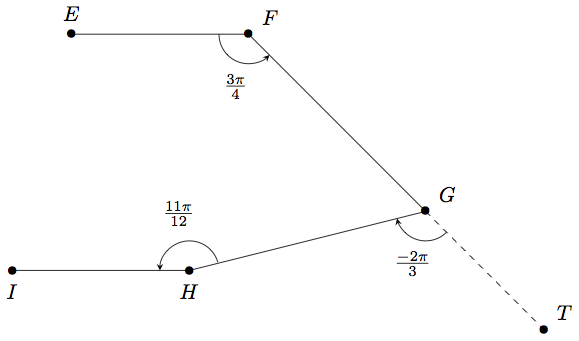

Question 1
Calculer l'angle .
Correction
Soient deux vecteurs et .
Les points et sont alignées car sur une même droite.- Si les vecteurs et sont colinéaires et de même sens alors l'angle orienté
- Si les vecteurs et sont colinéaires et de sens opposés alors l'angle orienté
De plus, les vecteurs et sont colinéaires et de sens opposés donc .
Or , donc d'après la relation de Chasles on a :
Ainsi :
Question 2
Calculer l'angle .
Correction
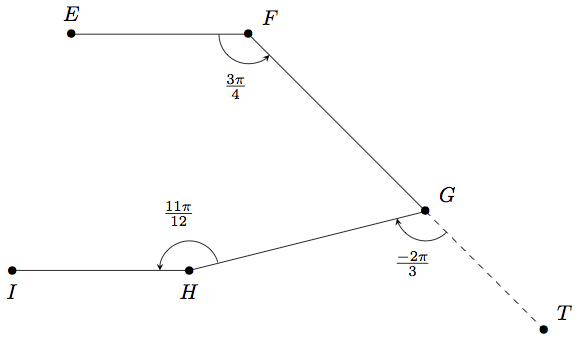
A l'aide de la représentation de la ligne brisée, on lit facilement que :
Or d'après la question , on sait que : , il vient alors que car .
On obtient dans ce cas :
On peut également écrire que :
.
Ce qui nous permet de dire que la mesure principale est alors :
Question 3
Que peut-on en déduire pour les droites et ?
Correction
Comme les vecteurs et sont donc colinéaires.
Les droites et sont donc parallèles.
Les droites et sont donc parallèles.
Signaler une erreur
Aide-nous à améliorer nos contenus en signalant les erreurs ou problèmes que tu penses avoir trouvés.
Connecte-toi ou crée un compte pour signaler une erreur.