Nouveau
🔥 Découvre nos fiches d'exercices gratuites avec corrections en vidéo !Accéder aux fiches →
Tchat avec un prof
🤔 Bloqué sur un exercice ou une notion de cours ? Échange avec un prof sur le tchat !Découvrir →
Exercices types : ère partie - Exercice 2
20 min
40
Dans le plan orienté, on considère la figure ci-dessous.
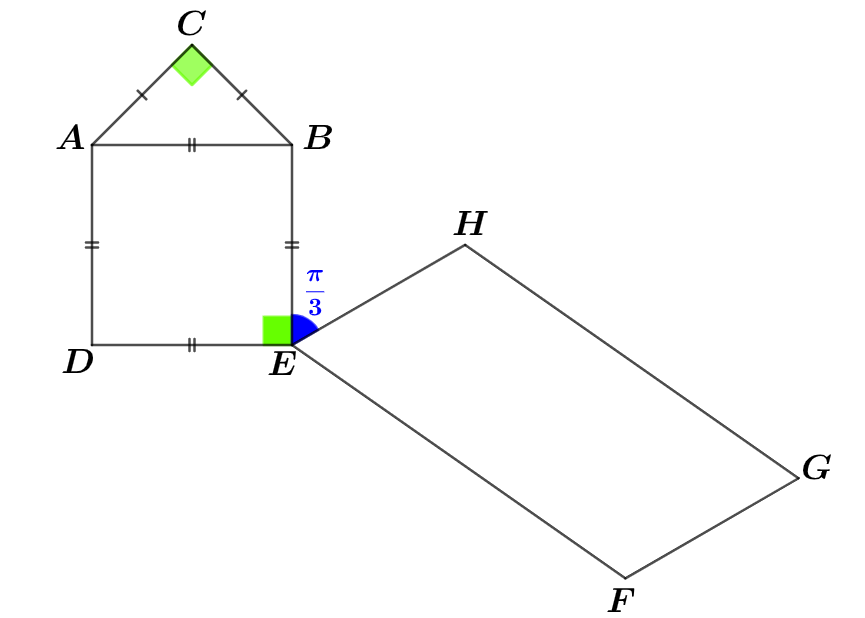

- est un triangle rectangle isocèle en tel que :
- est un carré tel que :
- est un parallélogramme.
Question 1
Déterminer la mesure principale des angles et
Correction
est un triangle rectangle isocèle en tel que : , il en résulte que les angles et sont égaux .
On rappelle que dans un triangle isocèle, les angles à la base sont égaux.
Ainsi .
Il en résulte donc que l'angle est dans le sens indirect soit .
Enfin , l'angle est dans le sens indirect soit :
Ainsi :
On rappelle que dans un triangle isocèle, les angles à la base sont égaux.
Ainsi .
Il en résulte donc que l'angle est dans le sens indirect soit .
Enfin , l'angle est dans le sens indirect soit :
Ainsi :
Question 2
Justifier l'égalité
Correction
On sait que est un carré.
Ainsi :
De même, on sait que est un parallélogramme.
Ainsi :
Finalement :
Ainsi :
De même, on sait que est un parallélogramme.
Ainsi :
Finalement :
Question 3
En déduire la mesure principale de l'angle
Correction
Comme .
Il nous suffit de déterminer la mesure de l'angle pour obtenir celle de .
On sait que alors :
Or car
Ainsi :
Il en résulte donc que :
Il nous suffit de déterminer la mesure de l'angle pour obtenir celle de .
On sait que alors :
Or car
Ainsi :
Il en résulte donc que :
Question 4
Déduire des trois résultats précédents la mesure principale de l'angle .
Correction
d'après la relation de Chasles.
Or :
d'après la question 1
d'après la question 1
d'après la question 3
Il vient alors que :
Or :
d'après la question 1
d'après la question 1
d'après la question 3
Il vient alors que :
Signaler une erreur
Aide-nous à améliorer nos contenus en signalant les erreurs ou problèmes que tu penses avoir trouvés.
Connecte-toi ou crée un compte pour signaler une erreur.