Qui aura 20 en maths ?
💯 Teste ton niveau de maths et tente de gagner un des lots !S'inscrire au jeu →
Nouveau
🔥 Découvre nos fiches d'exercices gratuites avec corrections en vidéo !Accéder aux fiches →
Exercices types (tableaux) : ère partie - Exercice 1
20 min
40
Les élèves de Première d’un lycée se répartissent de la façon suivante :
On interroge un élève au hasard parmi les . Tous les élèves ont la même probabilité d’être interrogés.
On considère les évènements suivants :
: « l’élève interrogé est une fille »; : « l’élève interrogé est externe »; : « l’élève interrogé est demi-pensionnaire »; : « l’élève interrogé est interne ». Les résultats seront donnés sous forme de fractions irréductibles.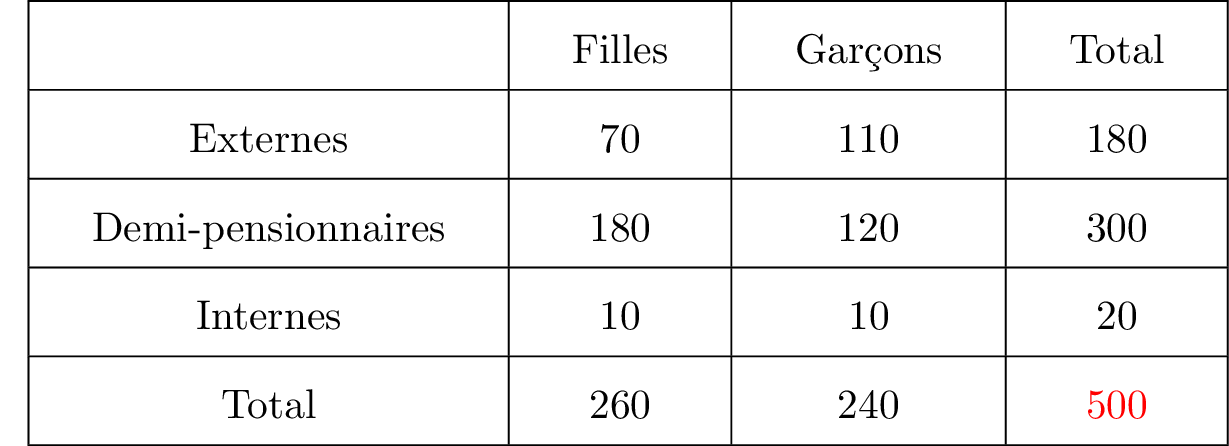
On interroge un élève au hasard parmi les . Tous les élèves ont la même probabilité d’être interrogés.
On considère les évènements suivants :

Question 1
Traduire par une phrase l’événement et calculer la probabilité .
Correction

Ainsi :
et l'on peut simplifier sous la forme
Question 2
Calculer la probabilité .
Correction
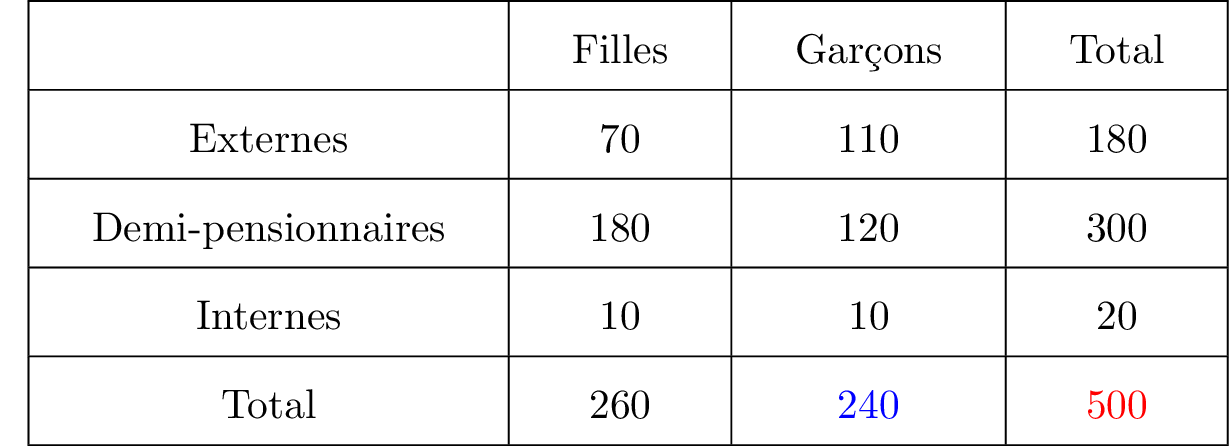
. Nous allons simplifier l'écriture de la fraction rationnelle . Il vient alors que :
Question 3
Calculer la probabilité .
Correction
L'évènement correspond à l'évènement : l’élève interrogé est externe l'élève est une fille.
 équivaut successivement à :
équivaut successivement à :
Ainsi :
Finalement :

Ainsi :
Finalement :
Question 4
Calculer la probabilité .
Correction

d'où :
Question 5
Calculer la probabilité .
Correction

. Nous allons simplifier l'écriture de la fraction rationnelle . Il vient alors que :
Question 6
Les évènements et sont ils indépendants ?
Correction
- Deux événements et sont indépendants si et seulement si :
-
Ainsi :
Il en résulte que les évènements et ne sont pas indépendants.