Déterminer le sens de variation d'une fonction polynôme de degré $$3$$ - Exercice 1

$$f'\left(x\right)=2\times3x^{2}-3\times2x-12$$
Ainsi :

Nous allons introduire une fonction $$h$$ définie et dérivable sur $$\left[-3;3\right]$$ tel que : $$h\left(x\right)=\left(2x-4\right)\left(3x+3\right)$$ .
Nous allons développer l'expression de la fonction $$h$$ et nous allons vérifier qu'elle est bien égale à $$f'$$.
$$h\left(x\right)=2x\times 3x+2x\times 3+\left(-4\right)\times 3x+\left(-4\right)\times 3$$
$$h\left(x\right)=6x^2+6x-12x-12$$
$$h\left(x\right)=6x^2-6x-12$$
Ainsi :
Il en résulte donc que pour tout réel $$x\in \left[-3;3\right]$$ : $$f'\left(x\right)=\left(2x-4\right)\left(3x+3\right)$$

Pour étudier le signe de $$f'\left(x\right)$$ nous allons étudier le signe de $$2x-4$$ et le signe de $$3x+3$$ .

D'une part :

$$2x-4=0\Leftrightarrow 2x=4\Leftrightarrow x=\frac{4}{2}=2$$
Soit $$x\mapsto 2x-4$$ est une fonction affine croissante car son coefficient directeur (taux d'accroissement) $$a=4>0$$. (Cela signifie que la fonction MONTE donc on commencera dans la ligne $$2x-4$$ par le signe $$\left(-\right)$$ et dès que l'on dépasse la valeur $$x=2$$ on mettra le signe $$\left(+\right)$$ dans le tableau de signe.)

D'autre part :

$$3x+3=0\Leftrightarrow 3x=-3\Leftrightarrow x=\frac{-3}{3}=-1$$
Soit $$x\mapsto 3x+3$$ est une fonction affine croissante car son coefficient directeur (taux d'accroissement) $$a=3>0$$. (Cela signifie que la fonction MONTE donc on commencera dans la ligne $$3x+3$$ par le signe $$\left(-\right)$$ et dès que l'on dépasse la valeur $$x=-1$$ on mettra le signe $$\left(+\right)$$ dans le tableau de signe.)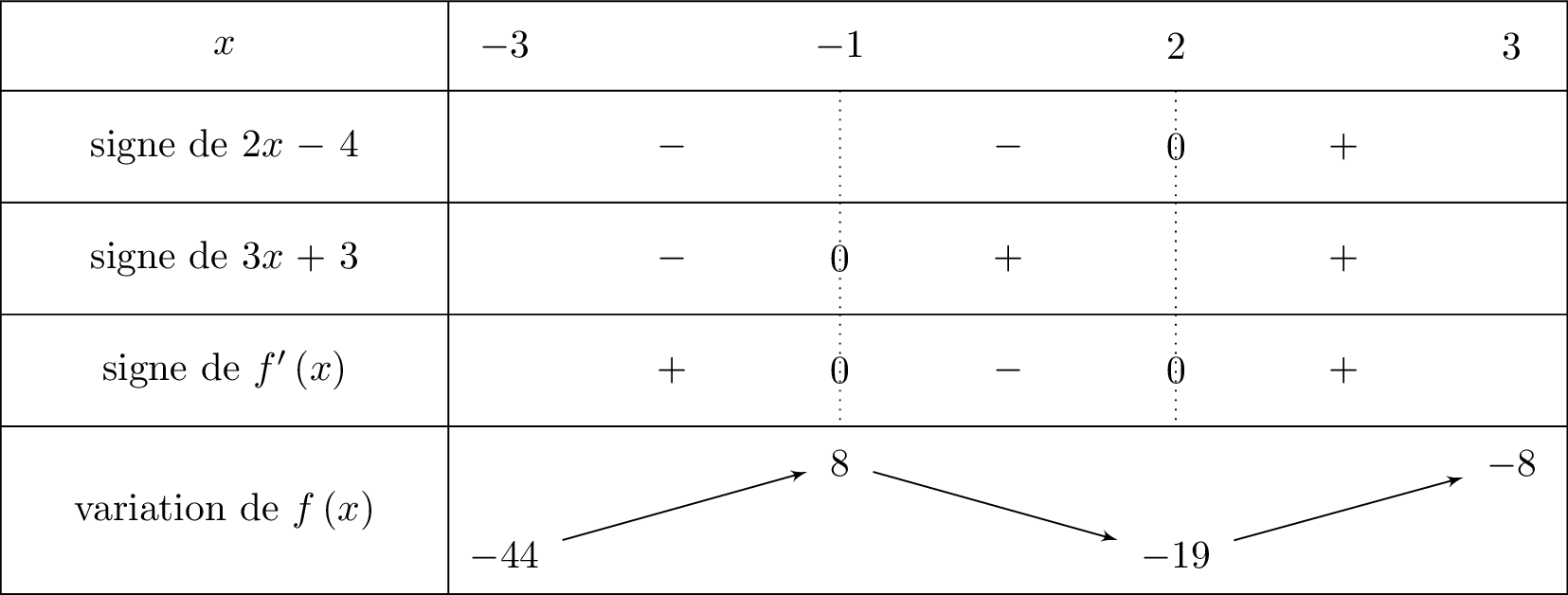De plus :

$$f\left(-3\right)=2\times\left(-3\right)^3-3\times\left(-3\right)^2-12\times\left(-3\right)+1 \Leftrightarrow f\left(-3\right)=-44$$

$$f\left(-1\right)=2\times\left(-1\right)^3-3\times\left(-1\right)^2-12\times\left(-1\right)+1 \Leftrightarrow f\left(-1\right)=8$$

$$f\left(2\right)=2\times2^3-3\times2^2-12\times2+1 \Leftrightarrow f\left(2\right)=-19$$

$$f\left(3\right)=2\times3^3-3\times3^2-12\times3+1 \Leftrightarrow f\left(3\right)=-8$$